Fehleroberfläche, lokale und globale Minima: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Elisa (Diskussion | Beiträge) |
||
| (3 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Nav|Navigation|Kognitive Modellierung|Hauptseite}} | {{Nav|Navigation|Fitting & Parameter Estimation|Kognitive Modellierung|Hauptseite}} | ||
== Was ist die Fehleroberfläche? == | == Was ist die Fehleroberfläche? == | ||
| Zeile 6: | Zeile 6: | ||
== Welche Probleme können bei der [[Fitting & Parameter Estimation|Optimierung]] auftreten? == | == Welche Probleme können bei der [[Fitting & Parameter Estimation|Optimierung]] auftreten? == | ||
[[Datei:Errorsurface.png]] | [[Datei:Errorsurface.png|link=Ausgelagerte_Bildbeschreibungen#Fehleroberfläche|Ausgelagerte Bildbeschreibung von Fehleroberfläche]] | ||
Beim Prozess des [[Fitting & Parameter Estimation|Data Fitting]] wird die Parameterausprägung gesucht, die den kleinstmöglichen Fehler mit sich bringt – also auf der Fehleroberfläche den niedrigsten Punkt aufweist, welcher als Minimum der Fehleroberfläche bezeichnet wird. Da die Fehleroberfläche in ihrer Gesamtheit unbekannt ist, tasten [[Algorithmen]] die Fehleroberfläche schrittweise ab, um dieses Minimum zu finden. Aufgrund des schrittweisen Vorgehens wird jedoch nicht für jede Parameterwertkombination das [[Abweichungsmaße|Abweichungsmaß]] berechnet. Dies ist aus zwei Gründen oftmals unmöglich: Erstens aus kombinatorischen Gründen, die eine genaue Abtastung schnell an die Grenzen der verfügbaren Rechenpower stoßen lassen. Wenn wir z.B. auch nur 3 Parameter haben und von diesen Parametern auch nur je 10 Stufen untersuchen wollen (also die Fehleroberfläche sehr grob abtasten möchten), so kommen wir bereits auf 10 x 10 x 10 = 1000 verschiedene Kombinationen und damit Modelldurchläufe, die notwendig sind, um den Fehler für jede Kombination zu errechnen. Entsprechend schnell stoßen selbst Hochleistungsrechner an ihre Grenzen, sollte jede erdenkliche Kombination geprüft werden müssen. Zweitens ist dies aber auch mathematisch nicht möglich, denn bei kontinuierlichen Parametern gibt es unendlich viele Ausprägungen jedes einzelnen Parameters. Es kann daher passieren, dass beim schrittweisen Abtasten der Fehleroberfläche bestimmte Abschnitte der Fehleroberfläche nicht beachtet werden. Ein [[Algorithmen|Algorithmus]] kann beispielsweise ein Minimum im durchsuchten Bereich entdecken, jedoch übersehen, dass sich an einer anderen Stelle ein noch tieferes – das wahre – Minimum befunden hätte. Letzteres wird als globales Minimum bezeichnet und ist eigentlich das Ziel des [[Fitting & Parameter Estimation|Data Fitting]]. Im Gegensatz dazu nennt man einen Tiefpunkt, der in einem umschriebenen Bereich der Fehleroberfläche liegt und weniger tief ist als das globale Minimum ein lokales Minimum. | Beim Prozess des [[Fitting & Parameter Estimation|Data Fitting]] wird die Parameterausprägung gesucht, die den kleinstmöglichen Fehler mit sich bringt – also auf der Fehleroberfläche den niedrigsten Punkt aufweist, welcher als Minimum der Fehleroberfläche bezeichnet wird. Da die Fehleroberfläche in ihrer Gesamtheit unbekannt ist, tasten [[Algorithmen]] die Fehleroberfläche schrittweise ab, um dieses Minimum zu finden. Aufgrund des schrittweisen Vorgehens wird jedoch nicht für jede Parameterwertkombination das [[Abweichungsmaße|Abweichungsmaß]] berechnet. Dies ist aus zwei Gründen oftmals unmöglich: Erstens aus kombinatorischen Gründen, die eine genaue Abtastung schnell an die Grenzen der verfügbaren Rechenpower stoßen lassen. Wenn wir z.B. auch nur 3 Parameter haben und von diesen Parametern auch nur je 10 Stufen untersuchen wollen (also die Fehleroberfläche sehr grob abtasten möchten), so kommen wir bereits auf 10 x 10 x 10 = 1000 verschiedene Kombinationen und damit Modelldurchläufe, die notwendig sind, um den Fehler für jede Kombination zu errechnen. Entsprechend schnell stoßen selbst Hochleistungsrechner an ihre Grenzen, sollte jede erdenkliche Kombination geprüft werden müssen. Zweitens ist dies aber auch mathematisch nicht möglich, denn bei kontinuierlichen Parametern gibt es unendlich viele Ausprägungen jedes einzelnen Parameters. Es kann daher passieren, dass beim schrittweisen Abtasten der Fehleroberfläche bestimmte Abschnitte der Fehleroberfläche nicht beachtet werden. Ein [[Algorithmen|Algorithmus]] kann beispielsweise ein Minimum im durchsuchten Bereich entdecken, jedoch übersehen, dass sich an einer anderen Stelle ein noch tieferes – das wahre – Minimum befunden hätte. Letzteres wird als globales Minimum bezeichnet und ist eigentlich das Ziel des [[Fitting & Parameter Estimation|Data Fitting]]. Im Gegensatz dazu nennt man einen Tiefpunkt, der in einem umschriebenen Bereich der Fehleroberfläche liegt und weniger tief ist als das globale Minimum ein lokales Minimum. | ||
Ein weiteres Problem bei der [[Fitting & Parameter Estimation|Optimierung]] können Sattelpunkte oder längere flache Bereiche der Fehleroberfläche darstellen. Einige [[Algorithmen]] arbeiten sich durch die Fehleroberfläche anhand von [[Gradient Descent|Gradienten]], das heißt anhand des Anstiegs der Fehlerfunktion, von Punkt zu Punkt nach unten ins Minimum. Wenn dieser Anstieg nur sehr flach ist, kann es sein, dass der [[Algorithmen|Algorithmus]], der immer dem steilsten Gradienten folgt, ein Abbruchkriterium erreicht. Er nimmt also an, dass er nun in einer Talsohle angekommen ist und erklärt die Suche an dieser Stelle für beendet. Die [[Fitting & Parameter Estimation|Optimierung]] bleibt dann sozusagen an der flachen Stelle stecken. | Ein weiteres Problem bei der [[Fitting & Parameter Estimation|Optimierung]] können Sattelpunkte oder längere flache Bereiche der Fehleroberfläche darstellen. Einige [[Algorithmen]] arbeiten sich durch die Fehleroberfläche anhand von [[Gradient Descent|Gradienten]], das heißt anhand des Anstiegs der Fehlerfunktion, von Punkt zu Punkt nach unten ins Minimum. Wenn dieser Anstieg nur sehr flach ist, kann es sein, dass der [[Algorithmen|Algorithmus]], der immer dem steilsten Gradienten folgt, ein Abbruchkriterium erreicht. Er nimmt also an, dass er nun in einer Talsohle angekommen ist und erklärt die Suche an dieser Stelle für beendet. Die [[Fitting & Parameter Estimation|Optimierung]] bleibt dann sozusagen an der flachen Stelle stecken. | ||
[[Datei:Simulationslink_neu2.PNG|link=http://141.76.19.82:3838/mediawiki/Fitting/fitting/ | |||
|120px]] <span style="color: white"> kkk </span> Die beschriebenen Probleme können in der R-Shiny-App [http://141.76.19.82:3838/mediawiki/Fitting/fitting/ "Fitting"] beobachtet und untersucht werden. | |||
== Was kann man dagegen tun? == | == Was kann man dagegen tun? == | ||
Bei der [[Fitting & Parameter Estimation|Optimierung]] mit [[Gradient Descent|gradientenbasierten Verfahren]] kann die Wahrscheinlichkeit, das globale Minimum der Fehleroberfläche zu finden, durch die Wahl verschiedener Startpositionen erhöht werden. Dabei ist es denkbar, ein gleichmäßiges Raster aus Startpositionen zu benutzen oder zufällige Startwerte zu wählen. Eine ähnliche Zufallskomponente steckt außerdem in nicht deterministischen [[Algorithmen|Optimierungsalgorithmen]], so zum Beispiel im [[Simulated Annealing]] oder in [[Genetische Algorithmen|genetischen Algorithmen]]. Dort sorgt sie dafür, dass lokale Minima auch wieder verlassen werden können und mit größerer Wahrscheinlichkeit – wenn auch nicht sicher – das globale Minimum gefunden wird. | Bei der [[Fitting & Parameter Estimation|Optimierung]] mit [[Gradient Descent|gradientenbasierten Verfahren]] kann die Wahrscheinlichkeit, das globale Minimum der Fehleroberfläche zu finden, durch die Wahl verschiedener Startpositionen erhöht werden. Dabei ist es denkbar, ein gleichmäßiges Raster aus Startpositionen zu benutzen oder zufällige Startwerte zu wählen. Eine ähnliche Zufallskomponente steckt außerdem in nicht deterministischen [[Algorithmen|Optimierungsalgorithmen]], so zum Beispiel im [[Simulated Annealing]] oder in [[Genetische Algorithmen|genetischen Algorithmen]]. Dort sorgt sie dafür, dass lokale Minima auch wieder verlassen werden können und mit größerer Wahrscheinlichkeit – wenn auch nicht sicher – das globale Minimum gefunden wird. | ||
Aktuelle Version vom 4. Dezember 2021, 14:40 Uhr
Was ist die Fehleroberfläche?
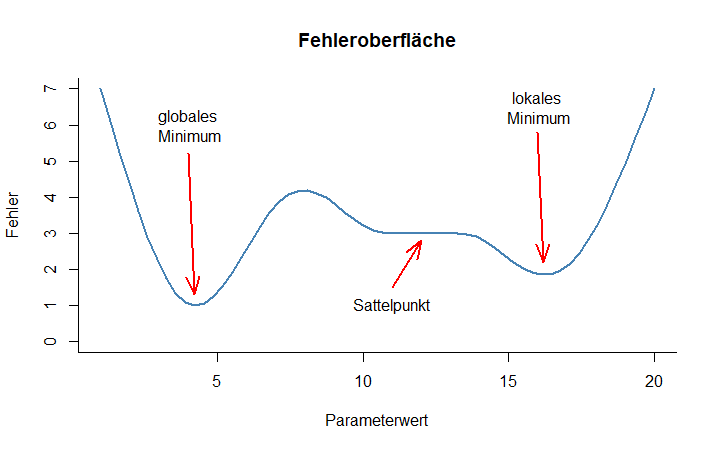
Die Fehleroberfläche ist die üblicherweise unbekannte Kurve oder Fläche, die entsteht, wenn für jeden Parameter bzw. jede Parameterkombination des Modells ein Abweichungsmaß zwischen Modell und Daten berechnet wird. Dafür eignen sich beispielsweise die Quadratfehlersumme (SSE) oder die maximale Plausibilität (MLE). Mit jedem Parameter kommt eine Dimension der Fehleroberfläche hinzu. Bei nur einem variierenden Parameter lässt sie sich, wie in der Abbildung, in einem zweidimensionalen Koordinatensystem darstellen. Anhand der Fehleroberfläche lässt sich nun leicht sehen, welche Probleme beim Data Fitting auftreten können.
Welche Probleme können bei der Optimierung auftreten?
Beim Prozess des Data Fitting wird die Parameterausprägung gesucht, die den kleinstmöglichen Fehler mit sich bringt – also auf der Fehleroberfläche den niedrigsten Punkt aufweist, welcher als Minimum der Fehleroberfläche bezeichnet wird. Da die Fehleroberfläche in ihrer Gesamtheit unbekannt ist, tasten Algorithmen die Fehleroberfläche schrittweise ab, um dieses Minimum zu finden. Aufgrund des schrittweisen Vorgehens wird jedoch nicht für jede Parameterwertkombination das Abweichungsmaß berechnet. Dies ist aus zwei Gründen oftmals unmöglich: Erstens aus kombinatorischen Gründen, die eine genaue Abtastung schnell an die Grenzen der verfügbaren Rechenpower stoßen lassen. Wenn wir z.B. auch nur 3 Parameter haben und von diesen Parametern auch nur je 10 Stufen untersuchen wollen (also die Fehleroberfläche sehr grob abtasten möchten), so kommen wir bereits auf 10 x 10 x 10 = 1000 verschiedene Kombinationen und damit Modelldurchläufe, die notwendig sind, um den Fehler für jede Kombination zu errechnen. Entsprechend schnell stoßen selbst Hochleistungsrechner an ihre Grenzen, sollte jede erdenkliche Kombination geprüft werden müssen. Zweitens ist dies aber auch mathematisch nicht möglich, denn bei kontinuierlichen Parametern gibt es unendlich viele Ausprägungen jedes einzelnen Parameters. Es kann daher passieren, dass beim schrittweisen Abtasten der Fehleroberfläche bestimmte Abschnitte der Fehleroberfläche nicht beachtet werden. Ein Algorithmus kann beispielsweise ein Minimum im durchsuchten Bereich entdecken, jedoch übersehen, dass sich an einer anderen Stelle ein noch tieferes – das wahre – Minimum befunden hätte. Letzteres wird als globales Minimum bezeichnet und ist eigentlich das Ziel des Data Fitting. Im Gegensatz dazu nennt man einen Tiefpunkt, der in einem umschriebenen Bereich der Fehleroberfläche liegt und weniger tief ist als das globale Minimum ein lokales Minimum.
Ein weiteres Problem bei der Optimierung können Sattelpunkte oder längere flache Bereiche der Fehleroberfläche darstellen. Einige Algorithmen arbeiten sich durch die Fehleroberfläche anhand von Gradienten, das heißt anhand des Anstiegs der Fehlerfunktion, von Punkt zu Punkt nach unten ins Minimum. Wenn dieser Anstieg nur sehr flach ist, kann es sein, dass der Algorithmus, der immer dem steilsten Gradienten folgt, ein Abbruchkriterium erreicht. Er nimmt also an, dass er nun in einer Talsohle angekommen ist und erklärt die Suche an dieser Stelle für beendet. Die Optimierung bleibt dann sozusagen an der flachen Stelle stecken.
kkk Die beschriebenen Probleme können in der R-Shiny-App "Fitting" beobachtet und untersucht werden.
Was kann man dagegen tun?
Bei der Optimierung mit gradientenbasierten Verfahren kann die Wahrscheinlichkeit, das globale Minimum der Fehleroberfläche zu finden, durch die Wahl verschiedener Startpositionen erhöht werden. Dabei ist es denkbar, ein gleichmäßiges Raster aus Startpositionen zu benutzen oder zufällige Startwerte zu wählen. Eine ähnliche Zufallskomponente steckt außerdem in nicht deterministischen Optimierungsalgorithmen, so zum Beispiel im Simulated Annealing oder in genetischen Algorithmen. Dort sorgt sie dafür, dass lokale Minima auch wieder verlassen werden können und mit größerer Wahrscheinlichkeit – wenn auch nicht sicher – das globale Minimum gefunden wird.