Abweichungsmaße: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Paul (Diskussion | Beiträge) (Abweichungsmaße Link einfügen pb) |
||
| (Eine dazwischenliegende Version von einem anderen Benutzer wird nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
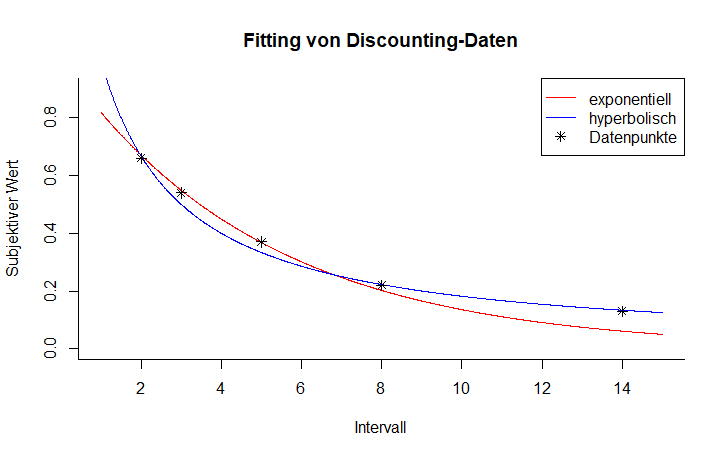
Der Prozess des [[Fitting & Parameter Estimation|Fittings]] versucht zu ermitteln, welches Modell mit welchen Parametern einen Datensatz am besten beschreibt, indem Modelle mit verschiedenen Parametern erstellt und mit den Daten verglichen werden. Doch wie kann diese Passung bestimmt werden? Die nachfolgende Abbildung zeigt Datenpunkte eines Discounting-Experiments und zwei mögliche Modelle zur Beschreibung dieser Daten. Die rote exponentielle Discounting-Kurve verläuft recht genau durch die ersten drei Punkte, während die blaue hyperbolische Discounting-Kurve die letzten beiden Punkte besser erfasst. Es ist demnach schwierig, mittels Augenmaß zu bestimmen, welches Modell das geeignetere ist. Stattdessen kann die Passung durch ein Abweichungsmaß quantifiziert werden. | Der Prozess des [[Fitting & Parameter Estimation|Fittings]] versucht zu ermitteln, welches Modell mit welchen Parametern einen Datensatz am besten beschreibt, indem Modelle mit verschiedenen Parametern erstellt und mit den Daten verglichen werden. Doch wie kann diese Passung bestimmt werden? Die nachfolgende Abbildung zeigt Datenpunkte eines Discounting-Experiments und zwei mögliche Modelle zur Beschreibung dieser Daten. Die rote exponentielle Discounting-Kurve verläuft recht genau durch die ersten drei Punkte, während die blaue hyperbolische Discounting-Kurve die letzten beiden Punkte besser erfasst. Es ist demnach schwierig, mittels Augenmaß zu bestimmen, welches Modell das geeignetere ist. Stattdessen kann die Passung durch ein Abweichungsmaß quantifiziert werden. | ||
[[Datei:Fit_discounting.png]] | [[Datei:Fit_discounting.png|link=Ausgelagerte_Bildbeschreibungen#Abweichungsmaße|Ausgelagerte Bildbeschreibung von Abweichungsmaße]] | ||
Abweichungsmaße geben an, wie gut die Daten des Modells und der empirischen Erhebung übereinstimmen. Besonders gebräuchlich sind dabei die [[SSE|Fehlerquadratsumme (Sum of Squared Errors)]] und die [[MLE|maximale Plausibilität (Maximum Likelihood)]]. | Abweichungsmaße geben an, wie gut die Daten des Modells und der empirischen Erhebung übereinstimmen. Besonders gebräuchlich sind dabei die [[SSE|Fehlerquadratsumme (Sum of Squared Errors)]] und die [[MLE|maximale Plausibilität (Maximum Likelihood)]]. | ||
Die Entstehung der Fehleroberfläche aus diesen Abweichungsmaßen wird in der R-Shiny-App [http://141.76.19.82:3838/mediawiki/Fitting/fitting/ "Fitting"] veranschaulicht. | [[Datei:Simulationslink_neu2.PNG|link=http://141.76.19.82:3838/mediawiki/Fitting/fitting/ | ||
|120px]] <span style="color: white"> kkk </span> Die Entstehung der Fehleroberfläche aus diesen Abweichungsmaßen wird in der R-Shiny-App [http://141.76.19.82:3838/mediawiki/Fitting/fitting/ "Fitting"] veranschaulicht. | |||
Aktuelle Version vom 18. Januar 2022, 12:50 Uhr
Der Prozess des Fittings versucht zu ermitteln, welches Modell mit welchen Parametern einen Datensatz am besten beschreibt, indem Modelle mit verschiedenen Parametern erstellt und mit den Daten verglichen werden. Doch wie kann diese Passung bestimmt werden? Die nachfolgende Abbildung zeigt Datenpunkte eines Discounting-Experiments und zwei mögliche Modelle zur Beschreibung dieser Daten. Die rote exponentielle Discounting-Kurve verläuft recht genau durch die ersten drei Punkte, während die blaue hyperbolische Discounting-Kurve die letzten beiden Punkte besser erfasst. Es ist demnach schwierig, mittels Augenmaß zu bestimmen, welches Modell das geeignetere ist. Stattdessen kann die Passung durch ein Abweichungsmaß quantifiziert werden.
Abweichungsmaße geben an, wie gut die Daten des Modells und der empirischen Erhebung übereinstimmen. Besonders gebräuchlich sind dabei die Fehlerquadratsumme (Sum of Squared Errors) und die maximale Plausibilität (Maximum Likelihood).
kkk Die Entstehung der Fehleroberfläche aus diesen Abweichungsmaßen wird in der R-Shiny-App "Fitting" veranschaulicht.