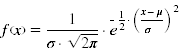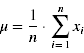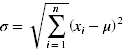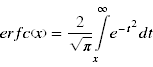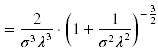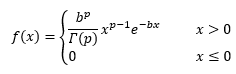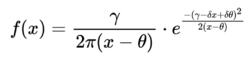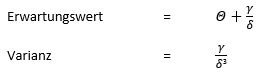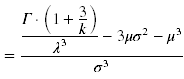Verteilungsmodelle: Unterschied zwischen den Versionen
Wehner (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
Paul (Diskussion | Beiträge) (→Weibullverteilung: link einfügen pb) |
||
| (29 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 6: | Zeile 6: | ||
Die Verteilungen vieler empirischer Variablen können mit Hilfe von statistischen Verteilungsmodellen näherungsweise beschrieben werden. Diese Modelle erlauben die Ermittlung charakteristischer Verteilungsmerkmale wie zum Beispiel des Erwartungswertes, der Varianz oder Prozentanteile bestimmter Wertebereiche (= Perzentile) und geben einen Überblick darüber, wie die empirischen Daten aussehen müssten, wenn deren Verteilung bestimmte Merkmale erfüllt. | Die Verteilungen vieler empirischer Variablen können mit Hilfe von statistischen Verteilungsmodellen näherungsweise beschrieben werden. Diese Modelle erlauben die Ermittlung charakteristischer Verteilungsmerkmale wie zum Beispiel des Erwartungswertes, der Varianz oder Prozentanteile bestimmter Wertebereiche (= Perzentile) und geben einen Überblick darüber, wie die empirischen Daten aussehen müssten, wenn deren Verteilung bestimmte Merkmale erfüllt. | ||
[[Datei:Simulationslink_neu2.PNG|120px]] <span style="color: white"> kkk </span> Einen Überblick über verschiedene Verteilungsmodelle erhalten Sie im Rahmen der Simulation [http://141.76.19.82:3838/mediawiki/ | [[Datei:Simulationslink_neu2.PNG|link=http://141.76.19.82:3838/mediawiki/Statistische_Modelle_Endversion/|120px]] <span style="color: white"> kkk </span> Einen Überblick über verschiedene Verteilungsmodelle erhalten Sie im Rahmen der Simulation [http://141.76.19.82:3838/mediawiki/Statistische_Modelle_Endversion/ Statistische Modelle]. | ||
Innerhalb der psychologischen Forschung kommen unterschiedliche Verteilungsmodelle beim Umgang mit z.B. Reaktionszeiten, Fehlerraten, IQ-Punkten etc. zum Einsatz. Sie sind der Verwendung einfacher statistischer Kenngrößen wie dem Mittelwert überlegen, da dieser insbesondere bei asymmetrischen und multimodalen Verteilungen zu fehlgeleiteten Schlussfolgerungen und Interpretationen führen kann. So ist es möglich, dass zwei unterschiedliche Verteilungen beispielsweise identische Mittelwerte und Standardabweichungen besitzen, sich aber aufgrund ihrer Schiefe stark unterscheiden. | Innerhalb der psychologischen Forschung kommen unterschiedliche Verteilungsmodelle beim Umgang mit z.B. Reaktionszeiten, Fehlerraten, IQ-Punkten etc. zum Einsatz. Sie sind der Verwendung einfacher statistischer Kenngrößen wie dem Mittelwert überlegen, da dieser insbesondere bei asymmetrischen und multimodalen Verteilungen zu fehlgeleiteten Schlussfolgerungen und Interpretationen führen kann. So ist es möglich, dass zwei unterschiedliche Verteilungen beispielsweise identische Mittelwerte und Standardabweichungen besitzen, sich aber aufgrund ihrer Schiefe stark unterscheiden. | ||
| Zeile 25: | Zeile 25: | ||
Man spricht von einer Normalverteilung, wenn eine stetige Zufallsvariable mit Erwartungswert μ und Varianz &sigma² (- ∞ < μ < ∞, σ² > 0) die folgende Dichtefunktion besitzt: | Man spricht von einer Normalverteilung, wenn eine stetige Zufallsvariable mit Erwartungswert μ und Varianz &sigma² (- ∞ < μ < ∞, σ² > 0) die folgende Dichtefunktion besitzt: | ||
::[[Datei: | ::[[Datei:Verteilungsmodelle_1_neu.png|link=Ausgelagerte_Formeln#Dichtefunktion Normalverteilung|Ausgelagerte Formel Dichtefunktion Normalverteilung]] | ||
Die Dichtefunktion dieser Verteilung wird in der folgenden Abbildung für verschiedene Erwartungswerte μ und Varianzen σ² dargestellt: | Die Dichtefunktion dieser Verteilung wird in der folgenden Abbildung für verschiedene Erwartungswerte μ und Varianzen σ² dargestellt: | ||
[[Datei:Verteilungsmodelle_2.png|600px]] | [[Datei:Verteilungsmodelle_2.png|600px|link=Ausgelagerte_Bildbeschreibungen#Verteilungsmodelle_Normalverteilung|Ausgelagerte Bildbeschreibung von Verteilungsmodelle Normalverteilung]] | ||
Der Graph der Normalverteilung ist glockenförmig und achsensymmetrisch, wobei der Parameter μ den Mittelwert der Verteilung darstellt, das heißt, die Werte der Zufallsvariablen konzentrieren sich in der Mitte der Verteilung und treten mit größerem Abstand zu dieser immer seltener auf. | Der Graph der Normalverteilung ist glockenförmig und achsensymmetrisch, wobei der Parameter μ den Mittelwert der Verteilung darstellt, das heißt, die Werte der Zufallsvariablen konzentrieren sich in der Mitte der Verteilung und treten mit größerem Abstand zu dieser immer seltener auf. | ||
| Zeile 37: | Zeile 37: | ||
Einen Vorteil der Normalverteilung stellt die einfache Schätzung der zwei Parameter μ und σ aus den empirischen Daten dar: | Einen Vorteil der Normalverteilung stellt die einfache Schätzung der zwei Parameter μ und σ aus den empirischen Daten dar: | ||
::[[Datei:Verteilungsmodelle_3_1.png]] , [[Datei:Verteilungsmodelle_3_2.png]] | ::[[Datei:Verteilungsmodelle_3_1.png|link=Ausgelagerte_Formeln#Schätzung My und Schätzung Sigma|Ausgelagerte Formel Schätzung My und Schätzung Sigma]] , [[Datei:Verteilungsmodelle_3_2.png|Das Bild ist Bestandteil der vorhergehenden Formel und wurde bereits dort beschrieben]] | ||
Unabhängig von μ und σ ist die Verteilung nicht schief, d.h. sie ist symmetrisch. | Unabhängig von μ und σ ist die Verteilung nicht schief, d.h. sie ist symmetrisch. | ||
Aufgrund ihrer Eigenschaften lässt sich die Normalverteilung jedoch nicht auf alle Daten anwenden, da Merkmale wie die Schiefe der Verteilung oder Ausreißerwerte nicht dargestellt werden können und somit kein guter Fit für entsprechende Daten erzielt werden kann. In solchen Fällen sollten andere Verteilungsmodelle verwendet werden. | Aufgrund ihrer Eigenschaften lässt sich die Normalverteilung jedoch nicht auf alle Daten anwenden, da Merkmale wie die Schiefe der Verteilung oder Ausreißerwerte nicht dargestellt werden können und somit kein guter Fit für entsprechende Daten erzielt werden kann. In solchen Fällen sollten andere Verteilungsmodelle verwendet werden. | ||
== Ex-Gauß Verteilung == | == Ex-Gauß Verteilung == | ||
| Zeile 50: | Zeile 49: | ||
Man spricht von einer Ex-Gauß Verteilung, wenn eine stetige Zufallsvariable die folgende Dichtefunktion mit den drei Parametern μ, σ und λ besitzt (σ² > 0, λ² > 0): | Man spricht von einer Ex-Gauß Verteilung, wenn eine stetige Zufallsvariable die folgende Dichtefunktion mit den drei Parametern μ, σ und λ besitzt (σ² > 0, λ² > 0): | ||
::[[Datei:Verteilungsmodelle_4.png]] | ::[[Datei:Verteilungsmodelle_4.png|link=Ausgelagerte_Formeln#Dichtefunktion Ex-Gauß-Verteilung|Ausgelagerte Formel Dichtefunktion Ex-Gauß-Verteilung]] | ||
Die komplementäre Fehlerfunktion ist: | Die komplementäre Fehlerfunktion ist: | ||
::[[Datei:Verteilungsmodelle_5.png]] | ::[[Datei:Verteilungsmodelle_5.png|link=Ausgelagerte_Formeln#Komplementäre Fehlerfunktion Ex-Gauß|Ausgelagerte Formel komplementäre Fehlerfunktion Ex Gauß]] | ||
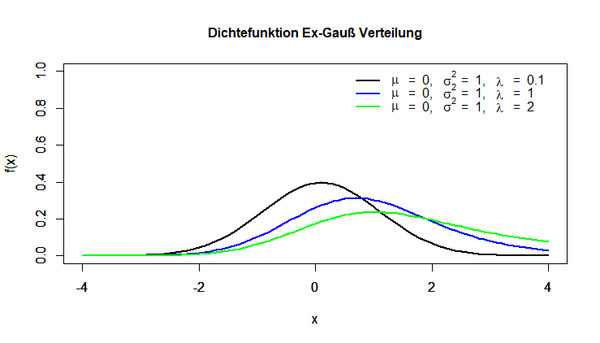
Die Dichtefunktion der Ex-Gauß Verteilung wird in der folgenden Abbildung dargestellt: | Die Dichtefunktion der Ex-Gauß Verteilung wird in der folgenden Abbildung dargestellt: | ||
[[Datei:Verteilungsmodelle_6.png|600px]] | [[Datei:Verteilungsmodelle_6.png|600px|link=Ausgelagerte_Bildbeschreibungen#Dichtefunktion_Ex-Gauß_Verteilung|Ausgelagerte Bildbeschreibung von Dichtefunktion Ex-Gauß Verteilung]] | ||
Der Parameter λ ist als λ > 0 definiert. Er stellt die exponentielle Komponente der Verteilung dar. Wie man in der Abbildung erkennen kann, ist die Ähnlichkeit der Ex-Gauß Verteilung und Normalverteilung abhängig vom Wert des Parameters λ. Je stärker sich dieser Parameter dem Wert Null annähert, desto mehr gleicht die Dichtefunktion dem Graphen der Normalverteilung. | Der Parameter λ ist als λ > 0 definiert. Er stellt die exponentielle Komponente der Verteilung dar. Wie man in der Abbildung erkennen kann, ist die Ähnlichkeit der Ex-Gauß Verteilung und Normalverteilung abhängig vom Wert des Parameters λ. Je stärker sich dieser Parameter dem Wert Null annähert, desto mehr gleicht die Dichtefunktion dem Graphen der Normalverteilung. | ||
| Zeile 66: | Zeile 65: | ||
::{| | ::{| | ||
| Mittelwert | | Mittelwert | ||
| [[Datei:Verteilungsmodelle_7.png]] | | [[Datei:Verteilungsmodelle_7.png|$=\mu+\frac{1}{\lambda}$]] | ||
|- | |- | ||
| Varianz | | Varianz | ||
| [[Datei:Verteilungsmodelle_8.png]] | | [[Datei:Verteilungsmodelle_8.png|$=\sigma^{2}+\frac{1}{\lambda^{2}}$]] | ||
|- | |- | ||
| Schiefe | | Schiefe | ||
| [[Datei:Verteilungsmodelle_9.png]] | | [[Datei:Verteilungsmodelle_9.png|$=\frac{2}{\sigma^{3} \lambda^{3}} \cdot\left(1+\frac{1}{\sigma^{2} \lambda^{2}}\right)^{-\frac{3}{2}}$]] | ||
|} | |} | ||
== Gammaverteilung == | == Gammaverteilung == | ||
| Zeile 80: | Zeile 78: | ||
Die Gammaverteilung ist ein Verteilungsmodell im Bereich der positiven reellen Zahlen. Es handelt sich um eine Gammaverteilung, wenn die Zufallsvariable die folgende Dichtefunktion f(x) mit den Parametern b > 0 und p > 0 besitzt: | Die Gammaverteilung ist ein Verteilungsmodell im Bereich der positiven reellen Zahlen. Es handelt sich um eine Gammaverteilung, wenn die Zufallsvariable die folgende Dichtefunktion f(x) mit den Parametern b > 0 und p > 0 besitzt: | ||
::[[Datei:Verteilungsmodelle_10_1.PNG]] | ::[[Datei:Verteilungsmodelle_10_1.PNG|link=Ausgelagerte_Formeln#Dichtefunktion Gammaverteilung|Ausgelagerte Formel Dichtefunktion Gammaverteilung]] | ||
mit der Gammafunktion Γ(x) | mit der Gammafunktion Γ(x) | ||
::[[Datei:Verteilungsmodelle_10_2.png]] | ::[[Datei:Verteilungsmodelle_10_2.png|link=Ausgelagerte_Formeln#Gammafunktion|Ausgelagerte Formel Gammafunktion]] | ||
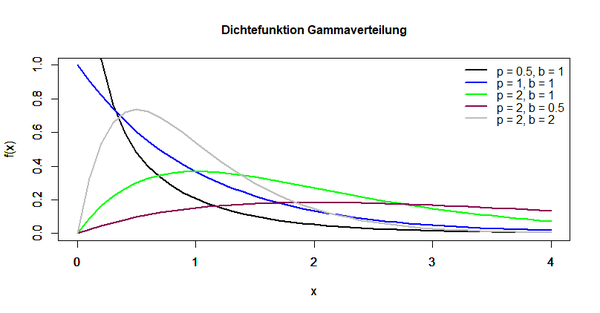
Die folgende Abbildung stellt die Dichtefunktion der Gammafunktion dar: | Die folgende Abbildung stellt die Dichtefunktion der Gammafunktion dar: | ||
[[Datei:Verteilungsmodelle_11.png|600px]] | [[Datei:Verteilungsmodelle_11.png|600px|link=Ausgelagerte_Bildbeschreibungen#Gammafunktion|Ausgelagerte Bildbeschreibung von Gammafunktion]] | ||
Erwartungswert, Varianz und Schiefe der Verteilung lassen sich durch die Wahl entsprechender Parameterwerte folgendermaßen ermitteln: | Erwartungswert, Varianz und Schiefe der Verteilung lassen sich durch die Wahl entsprechender Parameterwerte folgendermaßen ermitteln: | ||
::[[Datei:Verteilungsmodelle_12.PNG]] | ::[[Datei:Verteilungsmodelle_12.PNG|link=Ausgelagerte_Formeln#Gammaverteilung: Erwartungswert, Varianz, Schiefe|Ausgelagerte Formeln Erwartungswert, Varianz, Schiefe: Gammaverteilung]] | ||
Für p > 1 besitzt der Graph der Verteilung ein Maximum an der Stelle xmax = (p-1)/b. Wählt man den Parameterwert p = 1, erhält man eine Exponentialverteilung mit dem exponentiellen Parameter λ = b. | Für p > 1 besitzt der Graph der Verteilung ein Maximum an der Stelle xmax = (p-1)/b. Wählt man den Parameterwert p = 1, erhält man eine Exponentialverteilung mit dem exponentiellen Parameter λ = b. | ||
Einsatzmöglichkeiten der Gammaverteilung finden sich beispielsweise bei Reaktionszeitverteilungen sowie bei der Beschreibung der zufälligen Zeitdauer zwischen Ereignissen wie Unfällen. | Einsatzmöglichkeiten der Gammaverteilung finden sich beispielsweise bei Reaktionszeitverteilungen sowie bei der Beschreibung der zufälligen Zeitdauer zwischen Ereignissen wie Unfällen. | ||
== Shifted-Wald Verteilung == | == Shifted-Wald Verteilung == | ||
| Zeile 105: | Zeile 102: | ||
Sie ist durch die folgende Dichtefunktion mit den Parametern γ, δ und θ für x > θ definiert: | Sie ist durch die folgende Dichtefunktion mit den Parametern γ, δ und θ für x > θ definiert: | ||
::[[Datei: | ::[[Datei:SW_neu.png|250px|link=Ausgelagerte_Formeln#Dichtefunktion Shifted-Wald Verteilung|Ausgelagerte Formel Dichtefunktion Shifted-Wald Verteilung]] | ||
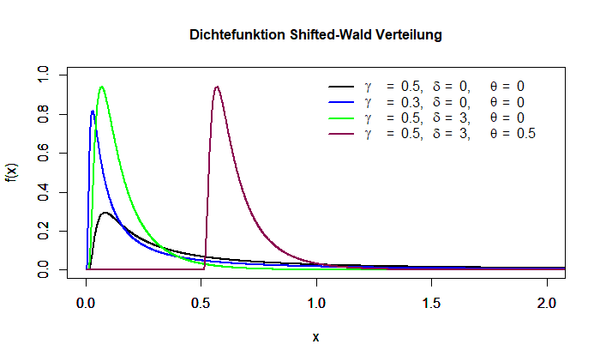
Die folgende Abbildung stellt die Dichtefunktion der Shifted-Wald Verteilung dar: | Die folgende Abbildung stellt die Dichtefunktion der Shifted-Wald Verteilung dar: | ||
[[Datei:Verteilungsmodelle_14.png|600px]] | [[Datei:Verteilungsmodelle_14.png|600px|link=Ausgelagerte_Bildbeschreibungen#Shifted-Wald_Verteilung|Ausgelagerte Bildbeschreibung von Shifted-Wald Verteilung]] | ||
Erwartungswert und Varianz der Verteilung sind folgendermaßen zu ermitteln: | Erwartungswert und Varianz der Verteilung sind folgendermaßen zu ermitteln: | ||
::[[Datei:Verteilungsmodelle_15.PNG]] | ::[[Datei:Verteilungsmodelle_15.PNG|link=Ausgelagerte_Formeln#Shifted-Wald Verteilung: Erwartungswert, Varianz|Ausgelagerte Formeln Erwartungswert und Varianz der Shifted-Wald Verteilung]] | ||
Der Parameter γ variiert dabei die Streuung der Verteilung um den Modalwert, der Parameter δ beeinflusst, wie viele Werte sich im rechten Teil der Verteilung befinden und der Parameter θ legt den Onset der Verteilung fest. | Der Parameter γ variiert dabei die Streuung der Verteilung um den Modalwert, der Parameter δ beeinflusst, wie viele Werte sich im rechten Teil der Verteilung befinden und der Parameter θ legt den Onset der Verteilung fest. | ||
== Weibullverteilung == | |||
Die Weibullverteilung ist ein Verteilungsmodell im Bereich der positiven reellen Zahlen. Man spricht von einer Weibullverteilung, wenn die Zufallsvariable die folgende Dichtefunktion f(x) mit den Parametern k > 0 und λ > 0 besitzt: | |||
Die | |||
::[[Datei:Verteilungsmodelle_16.png]] | ::[[Datei:Verteilungsmodelle_16.png|link=Ausgelagerte_Formeln#Dichtefunktion Weibullverteilung|Ausgelagerte Formel Dichtefunktion Weibullverteilung]] | ||
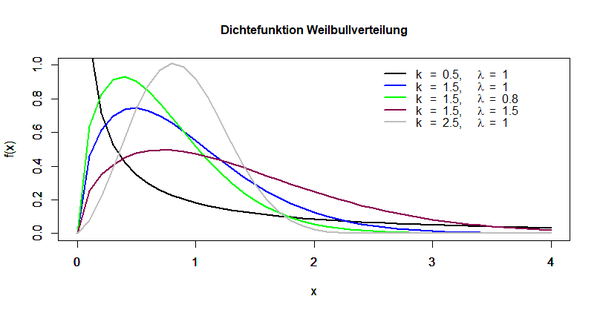
Die folgende Abbildung stellt die Dichtefunktion der | Die folgende Abbildung stellt die Dichtefunktion der Weibullverteilung dar: | ||
[[Datei:Verteilungsmodelle_17.png|600px]] | [[Datei:Verteilungsmodelle_17.png|600px|link=Ausgelagerte_Bildbeschreibungen#Weibullverteilung|Ausgelagerte Bildbeschreibung von Weibullverteilung]] | ||
Der Parameter k wird als Formparameter bezeichnet und der Parameter λ entspricht dem Skalen- oder Skalierungsparameter. Werden für diese Parameter bestimmte Werte ausgewählt, ähnelt die Verteilung einer Normal-, Exponential- oder anderen asymmetrischen Verteilung: | Der Parameter k wird als Formparameter bezeichnet und der Parameter λ entspricht dem Skalen- oder Skalierungsparameter. Werden für diese Parameter bestimmte Werte ausgewählt, ähnelt die Verteilung einer Normal-, Exponential- oder anderen asymmetrischen Verteilung: | ||
| Zeile 140: | Zeile 136: | ||
|} | |} | ||
Erwartungswert, Varianz und Schiefe der Verteilung lassen sich folgendermaßen ermitteln (Mittelwert μ = E(X) und Standardabweichung [[Datei:Verteilungsmodelle_18.png]]): | Erwartungswert, Varianz und Schiefe der Verteilung lassen sich folgendermaßen ermitteln (Mittelwert μ = E(X) und Standardabweichung [[Datei:Verteilungsmodelle_18.png|$\sigma=\sqrt{Var(X)}$]]): | ||
::{| | ::{| | ||
| Erwartungswert | | Erwartungswert | ||
| | | | ||
| [[Datei:Verteilungsmodelle_20.png]] | | [[Datei:Verteilungsmodelle_20.png|$=\lambda^{-1} \cdot \Gamma\left(1+\frac{1}{k}\right)$]] | ||
|- | |- | ||
| Varianz | | Varianz | ||
| | | | ||
| [[Datei:Verteilungsmodelle_21.png]] | | [[Datei:Verteilungsmodelle_21.png|$=\lambda^{-2} \cdot\left[\Gamma \cdot\left(1+\frac{2}{k}\right)-\Gamma^{2} \cdot\left(1+\frac{1}{k}\right)\right]$]] | ||
|- | |- | ||
| Schiefe | | Schiefe | ||
| | | | ||
| [[Datei:Verteilungsmodelle_22.png]] | | [[Datei:Verteilungsmodelle_22.png|$=\frac{\frac{\Gamma \cdot\left(1+\frac{3}{k}\right)}{\lambda^{3}}-3 \mu \sigma^{2}-\mu^{3}}{\sigma^{3}}$]] | ||
|} | |} | ||
Dazu benötigt man die Gammafunktion Γ(x), welche auch der Gammaverteilung zugrunde liegt: | Dazu benötigt man die Gammafunktion Γ(x), welche auch der Gammaverteilung zugrunde liegt: | ||
::[[Datei:Verteilungsmodelle_10_2.png]] | ::[[Datei:Verteilungsmodelle_10_2.png|link=Ausgelagerte_Formeln#Gammafunktion|Ausgelagerte Formel Gammafunktion]] | ||
Die | Die Weibullverteilung eignet sich gut zur Beschreibung von Daten, bei welchen keine negativen Werte auftreten und deren Verteilungen nicht symmetrisch sind. Sie wird beispielsweise zur Modellierung von Windgeschwindigkeiten und für Lebensdaueruntersuchungen verwendet. | ||
Aktuelle Version vom 10. April 2022, 10:29 Uhr
Die Verteilungen vieler empirischer Variablen können mit Hilfe von statistischen Verteilungsmodellen näherungsweise beschrieben werden. Diese Modelle erlauben die Ermittlung charakteristischer Verteilungsmerkmale wie zum Beispiel des Erwartungswertes, der Varianz oder Prozentanteile bestimmter Wertebereiche (= Perzentile) und geben einen Überblick darüber, wie die empirischen Daten aussehen müssten, wenn deren Verteilung bestimmte Merkmale erfüllt.
kkk Einen Überblick über verschiedene Verteilungsmodelle erhalten Sie im Rahmen der Simulation Statistische Modelle.
Innerhalb der psychologischen Forschung kommen unterschiedliche Verteilungsmodelle beim Umgang mit z.B. Reaktionszeiten, Fehlerraten, IQ-Punkten etc. zum Einsatz. Sie sind der Verwendung einfacher statistischer Kenngrößen wie dem Mittelwert überlegen, da dieser insbesondere bei asymmetrischen und multimodalen Verteilungen zu fehlgeleiteten Schlussfolgerungen und Interpretationen führen kann. So ist es möglich, dass zwei unterschiedliche Verteilungen beispielsweise identische Mittelwerte und Standardabweichungen besitzen, sich aber aufgrund ihrer Schiefe stark unterscheiden.
Verteilungsmodelle liefern somit mehr Informationen und werden deshalb zum Auffinden der besten Beschreibung der Daten, der Untersuchung von Bedingungs- und Gruppenunterschieden sowie in der weiteren Analyse verwendet. Damit ermöglichen sie ein tieferes Verständnis der Datenstruktur.
Verteilungsmodelle beschreibt man mittels der sogenannten Verteilungsfunktion f(x). Diese gibt an, wie groß die Wahrscheinlichkeit ist, dass eine Zufallsvariable (z.B. Reaktionszeit, IQ, …) einen Wert gleich oder kleiner als x annimmt. Sie besitzt somit einen positiven Wertebereich im Intervall [0,1] und ist monoton steigend.
Um einen visuellen Eindruck der Verteilung zu erhalten, nutzt man die Dichtefunktion, welche die Ableitung der Verteilungsfunktion darstellt. Sie gibt an, in welchen Teilen des Definitionsbereichs der Zufallsvariablen die Werte am häufigsten vorkommen. Die Werte der Dichtefunktion sind ebenfalls alle positiv, können jedoch auch größer als 1 sein. Möchte man anhand der Dichtefunktion die Wahrscheinlichkeit bestimmen, dass eine Zufallsvariable einen Wert innerhalb eines bestimmten Intervalls [a, b] aufweist, berechnet man hierzu die Fläche unterhalb der Kurve zwischen den Grenzen a und b. Das so ermittelte Ergebnis entspricht der Differenz der Werte der Verteilungsfunktion an den Stellen b und a. Die Gesamtfläche unterhalb der Dichtefunktion hat immer einen Wert von 1, da die Wahrscheinlichkeit, dass eine Zufallsvariable irgendeinen Wert innerhalb ihres Definitionsbereichs aufweist, ebenfalls 1 beträgt.
Das bekannteste Verteilungsmodell stellt die Normalverteilung dar. Diese ist beispielsweise zur Beschreibung der IQ-Werte innerhalb einer Population sehr gut geeignet, kann aufgrund ihrer Symmetrieeigenschaft jedoch z.B. nur schlecht für Reaktionszeitverteilungen verwendet werden. In solchen Fällen ist es möglich, mit anderen Verteilungsmodellen einen besseren Fit der Daten zu erreichen. Im Fall der Reaktionszeitverteilung könnte man beispielsweise auf eine Gammaverteilung zurückgreifen.
Normalverteilung
Die Normalverteilung ist das bekannteste und am weitesten verbreitete Verteilungsmodell, da die Werte vieler Variablen, die in der Psychologie oder den Sozialwissenschaften erhoben werden, normalverteilt sind. Dazu gehören unter anderem Körpergröße und Gewicht, IQ, aber auch Abweichungen der Messwerte vom Erwartungswert in vielen natur-, wirtschafts- und ingenieurwissenschaftlichen Untersuchungen.
Man spricht von einer Normalverteilung, wenn eine stetige Zufallsvariable mit Erwartungswert μ und Varianz &sigma² (- ∞ < μ < ∞, σ² > 0) die folgende Dichtefunktion besitzt:
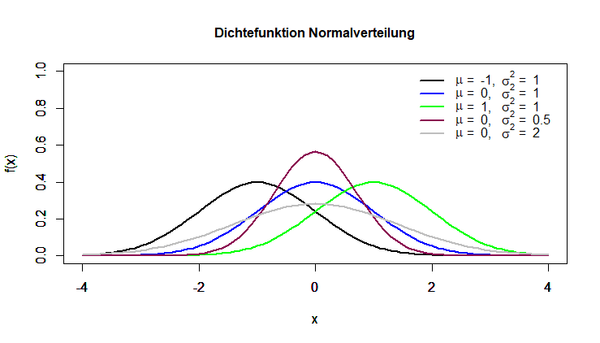
Die Dichtefunktion dieser Verteilung wird in der folgenden Abbildung für verschiedene Erwartungswerte μ und Varianzen σ² dargestellt:
Der Graph der Normalverteilung ist glockenförmig und achsensymmetrisch, wobei der Parameter μ den Mittelwert der Verteilung darstellt, das heißt, die Werte der Zufallsvariablen konzentrieren sich in der Mitte der Verteilung und treten mit größerem Abstand zu dieser immer seltener auf.
Die blaue Linie entspricht dabei der Dichtefunktion der Standardnormalverteilung. Diese ist durch den Erwartungswert μ = 0 und die Varianz σ² = 1 definiert.
Einen Vorteil der Normalverteilung stellt die einfache Schätzung der zwei Parameter μ und σ aus den empirischen Daten dar:
Unabhängig von μ und σ ist die Verteilung nicht schief, d.h. sie ist symmetrisch.
Aufgrund ihrer Eigenschaften lässt sich die Normalverteilung jedoch nicht auf alle Daten anwenden, da Merkmale wie die Schiefe der Verteilung oder Ausreißerwerte nicht dargestellt werden können und somit kein guter Fit für entsprechende Daten erzielt werden kann. In solchen Fällen sollten andere Verteilungsmodelle verwendet werden.
Ex-Gauß Verteilung
Die Ex-Gauß Verteilung stellt eine Konvolution oder Faltung (= mathematische Kombination) der Normal- und Exponentialverteilung dar. Sie liefert eine sehr gute Möglichkeit zur Schätzung von Reaktionszeiten und dient beispielsweise der Darstellung von Zellteilungsprozessen oder der Verdopplung der DNA.
Man spricht von einer Ex-Gauß Verteilung, wenn eine stetige Zufallsvariable die folgende Dichtefunktion mit den drei Parametern μ, σ und λ besitzt (σ² > 0, λ² > 0):
Die komplementäre Fehlerfunktion ist:
Die Dichtefunktion der Ex-Gauß Verteilung wird in der folgenden Abbildung dargestellt:
Der Parameter λ ist als λ > 0 definiert. Er stellt die exponentielle Komponente der Verteilung dar. Wie man in der Abbildung erkennen kann, ist die Ähnlichkeit der Ex-Gauß Verteilung und Normalverteilung abhängig vom Wert des Parameters λ. Je stärker sich dieser Parameter dem Wert Null annähert, desto mehr gleicht die Dichtefunktion dem Graphen der Normalverteilung.
Mittelwert, Varianz und Schiefe lassen sich folgendermaßen ermitteln:
Gammaverteilung
Die Gammaverteilung ist ein Verteilungsmodell im Bereich der positiven reellen Zahlen. Es handelt sich um eine Gammaverteilung, wenn die Zufallsvariable die folgende Dichtefunktion f(x) mit den Parametern b > 0 und p > 0 besitzt:
mit der Gammafunktion Γ(x)
Die folgende Abbildung stellt die Dichtefunktion der Gammafunktion dar:
Erwartungswert, Varianz und Schiefe der Verteilung lassen sich durch die Wahl entsprechender Parameterwerte folgendermaßen ermitteln:
Für p > 1 besitzt der Graph der Verteilung ein Maximum an der Stelle xmax = (p-1)/b. Wählt man den Parameterwert p = 1, erhält man eine Exponentialverteilung mit dem exponentiellen Parameter λ = b.
Einsatzmöglichkeiten der Gammaverteilung finden sich beispielsweise bei Reaktionszeitverteilungen sowie bei der Beschreibung der zufälligen Zeitdauer zwischen Ereignissen wie Unfällen.
Shifted-Wald Verteilung
Die Shifted-Wald Verteilung eignet sich aufgrund ihrer Eigenschaften sehr gut zur Beschreibung von Reaktionszeitdaten psychologischer Experimente. Sie besitzt drei Parameter und stellt eine um den Parameter θ auf der Abszissenachse verschobene Waldverteilung (= inverse Normalverteilung) dar.
Sie ist durch die folgende Dichtefunktion mit den Parametern γ, δ und θ für x > θ definiert:
Die folgende Abbildung stellt die Dichtefunktion der Shifted-Wald Verteilung dar:
Erwartungswert und Varianz der Verteilung sind folgendermaßen zu ermitteln:
Der Parameter γ variiert dabei die Streuung der Verteilung um den Modalwert, der Parameter δ beeinflusst, wie viele Werte sich im rechten Teil der Verteilung befinden und der Parameter θ legt den Onset der Verteilung fest.
Weibullverteilung
Die Weibullverteilung ist ein Verteilungsmodell im Bereich der positiven reellen Zahlen. Man spricht von einer Weibullverteilung, wenn die Zufallsvariable die folgende Dichtefunktion f(x) mit den Parametern k > 0 und λ > 0 besitzt:
Die folgende Abbildung stellt die Dichtefunktion der Weibullverteilung dar:
Der Parameter k wird als Formparameter bezeichnet und der Parameter λ entspricht dem Skalen- oder Skalierungsparameter. Werden für diese Parameter bestimmte Werte ausgewählt, ähnelt die Verteilung einer Normal-, Exponential- oder anderen asymmetrischen Verteilung:
| k = 1 | → | Exponentialverteilung |
| k ≈ 3.602 | → | Verteilung mit verschwindender Schiefe (ähnlich Normalverteilung) |
Erwartungswert, Varianz und Schiefe der Verteilung lassen sich folgendermaßen ermitteln (Mittelwert μ = E(X) und Standardabweichung ![]() ):
):
Dazu benötigt man die Gammafunktion Γ(x), welche auch der Gammaverteilung zugrunde liegt:
Die Weibullverteilung eignet sich gut zur Beschreibung von Daten, bei welchen keine negativen Werte auftreten und deren Verteilungen nicht symmetrisch sind. Sie wird beispielsweise zur Modellierung von Windgeschwindigkeiten und für Lebensdaueruntersuchungen verwendet.