Hierarchische Regression: Unterschied zwischen den Versionen
Wehner (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
Elisa (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
||
| (Eine dazwischenliegende Version von einem anderen Benutzer wird nicht angezeigt) | |||
| Zeile 6: | Zeile 6: | ||
'''''Beispiel''''' | '''''Beispiel''''' | ||
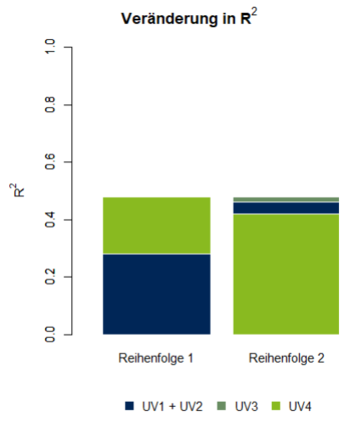
In einer multiplen linearen Regression mit 4 Prädiktoren sollen die individuellen Erklärungsbeiträge der Prädiktoren analysiert werden. Da die Prädiktoren untereinander korrelieren, können [[Multikollinearität| | In einer multiplen linearen Regression mit 4 Prädiktoren sollen die individuellen Erklärungsbeiträge der Prädiktoren analysiert werden. Da die Prädiktoren untereinander korrelieren, können [[Multikollinearität|Multikollinearitätseffekte]] nicht ausgeschlossen werden. Um diese zu untersuchen, werden zwei hierarchische Regressionen durchgeführt, in denen die Prädiktoren in verschiedenen Reihenfolgen in das Modell aufgenommen werden (Abbildung 1). | ||
[[File:3_6_Hierarchische_Regression.PNG|350px|Abbildung 1: Schrittweise Veränderung des multiplen Bestimmtheitsmaßes bei 2 hierarchischen Regressionen]] | [[File:3_6_Hierarchische_Regression.PNG|350px|Abbildung 1: Schrittweise Veränderung des multiplen Bestimmtheitsmaßes bei 2 hierarchischen Regressionen|link=Ausgelagerte_Bildbeschreibungen#Hierarchische_Regression|Ausgelagerte Bildbeschreibung von Hierarchische Regression]] | ||
In der ersten hierarchischen Regression wird dem Modell zunächst eine Merkmalsmenge aus den Prädiktoren 1 und 2 hinzugefügt. Eine multiple Regression mit diesen beiden Prädiktoren klärt 28% der Varianz des Kriteriums auf (p < 0.05). Fügt man Prädiktor 3 dem Modell hinzu, führt das zu keiner signifikanten Veränderung von R². Ein Modell, das zusätzlich Prädiktor 4 berücksichtigt, hat einen signifikant höheres multiples Bestimmtheitsmaß (ΔR² = 0.2; p < 0.01). In der ersten hierarchischen Regression tragen also sowohl die Merkmalsmenge aus Prädiktor 1 und 2 als auch Prädiktor 4 zur Varianzaufklärung bei. Fügt man in einer zweiten hierarchischen Regression die Prädiktoren in der Reihenfolge 4 → ‚1 & 2 ‘ → 3 dem Modell hinzu, übernimmt Prädiktor 4 im ersten Schritt 42% der 48% Gesamtvarianz des Modelles, sodass weder das Hinzufügen von Prädiktor 1 und 2 noch das Hinzufügen von Prädiktor 3 in weiteren Schritten signifikant zur Veränderung des Bestimmtheitsmaßes beitragen. Der größte Unterschied zur ersten hierarchischen Regression liegt in der geringeren Varianzaufklärung durch die Prädiktoren 1 und 2. Prädiktor 4 übernimmt im ersten Schritt bereits große Varianzanteile der Prädiktoren, sodass deren zusätzliche Aufnahme keinen weiteren Erklärungsbeitrag zur Vorhersage des Kriteriums liefert. Die Prädiktoren 1 und 2 sind in diesem Modell redundant. In Abhängigkeit von inhaltlichen Gesichtspunkten könnte in Betracht gezogen werden, den nichtrelevanten Prädiktor 3 und die redundanten Prädiktoren 1 und 2 aus dem Modell zu entfernen. | In der ersten hierarchischen Regression wird dem Modell zunächst eine Merkmalsmenge aus den Prädiktoren 1 und 2 hinzugefügt. Eine multiple Regression mit diesen beiden Prädiktoren klärt 28% der Varianz des Kriteriums auf (p < 0.05). Fügt man Prädiktor 3 dem Modell hinzu, führt das zu keiner signifikanten Veränderung von R². Ein Modell, das zusätzlich Prädiktor 4 berücksichtigt, hat einen signifikant höheres multiples Bestimmtheitsmaß (ΔR² = 0.2; p < 0.01). In der ersten hierarchischen Regression tragen also sowohl die Merkmalsmenge aus Prädiktor 1 und 2 als auch Prädiktor 4 zur Varianzaufklärung bei. Fügt man in einer zweiten hierarchischen Regression die Prädiktoren in der Reihenfolge 4 → ‚1 & 2 ‘ → 3 dem Modell hinzu, übernimmt Prädiktor 4 im ersten Schritt 42% der 48% Gesamtvarianz des Modelles, sodass weder das Hinzufügen von Prädiktor 1 und 2 noch das Hinzufügen von Prädiktor 3 in weiteren Schritten signifikant zur Veränderung des Bestimmtheitsmaßes beitragen. Der größte Unterschied zur ersten hierarchischen Regression liegt in der geringeren Varianzaufklärung durch die Prädiktoren 1 und 2. Prädiktor 4 übernimmt im ersten Schritt bereits große Varianzanteile der Prädiktoren, sodass deren zusätzliche Aufnahme keinen weiteren Erklärungsbeitrag zur Vorhersage des Kriteriums liefert. Die Prädiktoren 1 und 2 sind in diesem Modell redundant. In Abhängigkeit von inhaltlichen Gesichtspunkten könnte in Betracht gezogen werden, den nichtrelevanten Prädiktor 3 und die redundanten Prädiktoren 1 und 2 aus dem Modell zu entfernen. | ||
Aktuelle Version vom 5. Januar 2022, 16:57 Uhr
In der hierarchischen linearen Regression werden Prädiktoren und Prädiktormengen schrittweise in einer vorgegebenen Reihenfolge in das Modell aufgenommen, um deren spezifische Erklärungsbeiträge zu analysieren. Um bei multiplen linearen Regressionen die Relevanz einzelner Variablen zur Varianzaufklärung eines Modelles herauszufinden, bietet es sich an, die Prädiktoren schrittweise zum Regressionsmodell hinzuzufügen. Dabei kann betrachtet werden, inwieweit sich das multiple Bestimmtheitsmaß durch die Aufnahme einzelner Prädiktoren verändert. Die Reihenfolge, in der die Prädiktoren in ein Modell aufgenommen werden, ist von inhaltlichen Überlegungen abhängig. Bei Abhängigkeiten zwischen Prädiktoren können unterschiedlichen Reihenfolgen der Aufnahme in die hierarchischen Regressionen verglichen werden, um mögliche Redundanz- und Suppressionseffekte zu analysieren.
Beispiel
In einer multiplen linearen Regression mit 4 Prädiktoren sollen die individuellen Erklärungsbeiträge der Prädiktoren analysiert werden. Da die Prädiktoren untereinander korrelieren, können Multikollinearitätseffekte nicht ausgeschlossen werden. Um diese zu untersuchen, werden zwei hierarchische Regressionen durchgeführt, in denen die Prädiktoren in verschiedenen Reihenfolgen in das Modell aufgenommen werden (Abbildung 1).
In der ersten hierarchischen Regression wird dem Modell zunächst eine Merkmalsmenge aus den Prädiktoren 1 und 2 hinzugefügt. Eine multiple Regression mit diesen beiden Prädiktoren klärt 28% der Varianz des Kriteriums auf (p < 0.05). Fügt man Prädiktor 3 dem Modell hinzu, führt das zu keiner signifikanten Veränderung von R². Ein Modell, das zusätzlich Prädiktor 4 berücksichtigt, hat einen signifikant höheres multiples Bestimmtheitsmaß (ΔR² = 0.2; p < 0.01). In der ersten hierarchischen Regression tragen also sowohl die Merkmalsmenge aus Prädiktor 1 und 2 als auch Prädiktor 4 zur Varianzaufklärung bei. Fügt man in einer zweiten hierarchischen Regression die Prädiktoren in der Reihenfolge 4 → ‚1 & 2 ‘ → 3 dem Modell hinzu, übernimmt Prädiktor 4 im ersten Schritt 42% der 48% Gesamtvarianz des Modelles, sodass weder das Hinzufügen von Prädiktor 1 und 2 noch das Hinzufügen von Prädiktor 3 in weiteren Schritten signifikant zur Veränderung des Bestimmtheitsmaßes beitragen. Der größte Unterschied zur ersten hierarchischen Regression liegt in der geringeren Varianzaufklärung durch die Prädiktoren 1 und 2. Prädiktor 4 übernimmt im ersten Schritt bereits große Varianzanteile der Prädiktoren, sodass deren zusätzliche Aufnahme keinen weiteren Erklärungsbeitrag zur Vorhersage des Kriteriums liefert. Die Prädiktoren 1 und 2 sind in diesem Modell redundant. In Abhängigkeit von inhaltlichen Gesichtspunkten könnte in Betracht gezogen werden, den nichtrelevanten Prädiktor 3 und die redundanten Prädiktoren 1 und 2 aus dem Modell zu entfernen.
kkk Im Video wird die hierarchische Regression näher erläutert.
kkk In der interaktiven Simulation können hierarchische Regressionen an verschiedenen Datensätzen nachvollzogen werden.
Weiterführende Literatur
Bortz, J., & Schuster, C. (2016). Statistik für Human- und Sozialwissenschaftler. Berlin: Springer.
Eid, M., Gollwitzer, M., & Schmitt, M. (2017). Statistik und Forschungsmethoden. Weinheim: Beltz.
Rudolf, M. & Buse, J. (2020). Multivariate Verfahren. Eine praxisorientierte Einführung mit Anwendungsbeispielen (3. Aufl., Kapitel 2.2.3). Göttingen: Hogrefe.