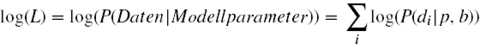MLE: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Paul (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
||
| (5 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
Maximum Likelihood Estimation (MLE) ist eine Methode zur [[Fitting & Parameter Estimation|Parameterschätzung]], bei der die Plausibilität (Likelihood) der empirischen Daten unter dem Vorliegen bestimmter Modellparameter berechnet wird. Sie gilt als effiziente Methode und eignet sich für beliebige Wahrscheinlichkeitsverteilungen. Voraussetzung ist lediglich, dass alle Datenpunkte der gleichen (bekannten) Verteilung entstammen und statistisch unabhängig voneinander sind. Außerdem muss das Modell korrekt spezifiziert sein, das heißt, die bedingten Wahrscheinlichkeiten sollten tatsächlich der angenommenen Verteilung folgen. Empfehlenswert ist zudem eine große Stichprobe von mindestens 100 Datenpunkten (Andres, 1996). Die Passung eines Modells zu den Daten wird dann als bedingte Wahrscheinlichkeit angegeben: P(Daten|Modellparameter). | Maximum Likelihood Estimation (MLE) ist eine Methode zur [[Fitting & Parameter Estimation|Parameterschätzung]], bei der die Plausibilität (Likelihood) der empirischen Daten unter dem Vorliegen bestimmter Modellparameter berechnet wird. Sie gilt als effiziente Methode und eignet sich für beliebige Wahrscheinlichkeitsverteilungen. Voraussetzung ist lediglich, dass alle Datenpunkte der gleichen (bekannten) Verteilung entstammen und statistisch unabhängig voneinander sind. Außerdem muss das Modell korrekt spezifiziert sein, das heißt, die bedingten Wahrscheinlichkeiten sollten tatsächlich der angenommenen Verteilung folgen. Empfehlenswert ist zudem eine große Stichprobe von mindestens 100 Datenpunkten (Andres, 1996). Die Passung eines Modells zu den Daten wird dann als bedingte Wahrscheinlichkeit angegeben: P(Daten|Modellparameter). | ||
[[Datei:Mle_estimation.png|550px]] | [[Datei:Mle_estimation.png|550px|link=Ausgelagerte_Bildbeschreibungen#MLE|Ausgelagerte Bildbeschreibung von MLE]] | ||
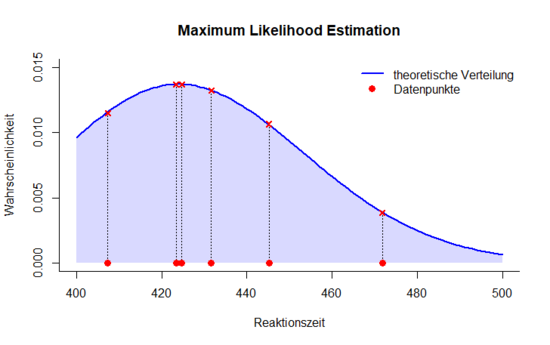
Die hier dargestellte Abbildung stellt Reaktionszeiten dar, von denen vermutet wird, dass sie aus einer [[Verteilungsmodelle#Gammaverteilung|Gammaverteilung]] mit den Parametern p und b stammen. Um nun die Plausibilität dieser Daten unter der Bedingung der gegebenen Parameterwerte zu bestimmen, werden zunächst die Wahrscheinlichkeiten der einzelnen Datenpunkte d<sub>i</sub> mithilfe einer [[Verteilungsmodelle#Gammaverteilung|Gammaverteilung]] mit bestimmten Parameterwerten geschätzt. Die gemeinsame Wahrscheinlichkeit (Likelihood) L der Datenpunkte ergibt sich durch die Multiplikation der Einzelwahrscheinlichkeiten: | Die hier dargestellte Abbildung stellt Reaktionszeiten dar, von denen vermutet wird, dass sie aus einer [[Verteilungsmodelle#Gammaverteilung|Gammaverteilung]] mit den Parametern p und b stammen. Um nun die Plausibilität dieser Daten unter der Bedingung der gegebenen Parameterwerte zu bestimmen, werden zunächst die Wahrscheinlichkeiten der einzelnen Datenpunkte d<sub>i</sub> mithilfe einer [[Verteilungsmodelle#Gammaverteilung|Gammaverteilung]] mit bestimmten Parameterwerten geschätzt. Die gemeinsame Wahrscheinlichkeit (Likelihood) L der Datenpunkte ergibt sich durch die Multiplikation der Einzelwahrscheinlichkeiten: | ||
| Zeile 12: | Zeile 12: | ||
Ein Nachteil der Maximum-Likelihood-Methode ist, dass das Endergebnis eine sehr kleine Zahl sein kann (im Beispiel der Abbildung 1,2 * 10<sup>-12</sup>) und dass die Multiplikation einen hohen Rechenaufwand verursacht. Daher wird meist auf die sogenannte Log-Likelihood zurückgegriffen. Für die Berechnung bedeutet das, dass nur die Logarithmen der einzelnen Wahrscheinlichkeiten aufsummiert werden müssen und keine Multiplikation mehr nötig ist. Das folgt aus dem Logarithmengesetz, welches besagt, dass der Logarithmus eines Produktes auch als Summe der Logarithmen der Faktoren geschrieben werden kann. Allgemein gesagt wird aus log(u*v) nun log(u)+log(v). Angewendet auf die Likelihoodfunktion wird aus dem Logarithmus des Produktes der Einzelwahrscheinlichkeiten log(∏P(d<sub>i</sub>|p,b)) nun die Summe: | Ein Nachteil der Maximum-Likelihood-Methode ist, dass das Endergebnis eine sehr kleine Zahl sein kann (im Beispiel der Abbildung 1,2 * 10<sup>-12</sup>) und dass die Multiplikation einen hohen Rechenaufwand verursacht. Daher wird meist auf die sogenannte Log-Likelihood zurückgegriffen. Für die Berechnung bedeutet das, dass nur die Logarithmen der einzelnen Wahrscheinlichkeiten aufsummiert werden müssen und keine Multiplikation mehr nötig ist. Das folgt aus dem Logarithmengesetz, welches besagt, dass der Logarithmus eines Produktes auch als Summe der Logarithmen der Faktoren geschrieben werden kann. Allgemein gesagt wird aus log(u*v) nun log(u)+log(v). Angewendet auf die Likelihoodfunktion wird aus dem Logarithmus des Produktes der Einzelwahrscheinlichkeiten log(∏P(d<sub>i</sub>|p,b)) nun die Summe: | ||
[[Datei:Mle2.png|480px]] | [[Datei:Mle2.png|480px|link=Ausgelagerte_Formeln#Log-Likelihood|Ausgelagerte Formel Log-Likelihood]] | ||
[[Datei:Simulationslink_neu2.PNG|link=http://141.76.19.82:3838/mediawiki/Fitting/fitting/ | [[Datei:Simulationslink_neu2.PNG|link=http://141.76.19.82:3838/mediawiki/Fitting/fitting/ | ||
|120px]] <span style="color: white"> kkk </span> Die Ermittlung der Fehleroberfläche mittels der MLE wird in der R-Shiny-App [http://141.76.19.82:3838/mediawiki/Fitting/fitting/ "Fitting"] veranschaulicht. | |120px]] <span style="color: white"> kkk </span> Die Ermittlung der Fehleroberfläche mittels der MLE wird in der R-Shiny-App [http://141.76.19.82:3838/mediawiki/Fitting/fitting/ "Fitting"] veranschaulicht. | ||
Aktuelle Version vom 18. Januar 2022, 12:45 Uhr
Maximum Likelihood Estimation (MLE) ist eine Methode zur Parameterschätzung, bei der die Plausibilität (Likelihood) der empirischen Daten unter dem Vorliegen bestimmter Modellparameter berechnet wird. Sie gilt als effiziente Methode und eignet sich für beliebige Wahrscheinlichkeitsverteilungen. Voraussetzung ist lediglich, dass alle Datenpunkte der gleichen (bekannten) Verteilung entstammen und statistisch unabhängig voneinander sind. Außerdem muss das Modell korrekt spezifiziert sein, das heißt, die bedingten Wahrscheinlichkeiten sollten tatsächlich der angenommenen Verteilung folgen. Empfehlenswert ist zudem eine große Stichprobe von mindestens 100 Datenpunkten (Andres, 1996). Die Passung eines Modells zu den Daten wird dann als bedingte Wahrscheinlichkeit angegeben: P(Daten|Modellparameter).
Die hier dargestellte Abbildung stellt Reaktionszeiten dar, von denen vermutet wird, dass sie aus einer Gammaverteilung mit den Parametern p und b stammen. Um nun die Plausibilität dieser Daten unter der Bedingung der gegebenen Parameterwerte zu bestimmen, werden zunächst die Wahrscheinlichkeiten der einzelnen Datenpunkte di mithilfe einer Gammaverteilung mit bestimmten Parameterwerten geschätzt. Die gemeinsame Wahrscheinlichkeit (Likelihood) L der Datenpunkte ergibt sich durch die Multiplikation der Einzelwahrscheinlichkeiten:
Die so bestimmte Likelihoodfunktion ist abhängig von den Parametern p und b der Gammaverteilung. Das Ziel beim Fitting ist es, die Parameter zu finden, für die die Likelihood am höchsten ist, da so die Verteilung bestimmt werden kann, der die Daten am ehesten entstammen. Beim Fitting mittels der Maximum-Likelihood-Methode ist zu beachten, dass Optimierungsalgorithmen darauf ausgelegt sind, das Minimum einer Funktion zu finden. Da der optimale Wert hier jedoch die maximale Wahrscheinlichkeit ist, müssen die Werte zuvor negativiert werden.
Ein Nachteil der Maximum-Likelihood-Methode ist, dass das Endergebnis eine sehr kleine Zahl sein kann (im Beispiel der Abbildung 1,2 * 10-12) und dass die Multiplikation einen hohen Rechenaufwand verursacht. Daher wird meist auf die sogenannte Log-Likelihood zurückgegriffen. Für die Berechnung bedeutet das, dass nur die Logarithmen der einzelnen Wahrscheinlichkeiten aufsummiert werden müssen und keine Multiplikation mehr nötig ist. Das folgt aus dem Logarithmengesetz, welches besagt, dass der Logarithmus eines Produktes auch als Summe der Logarithmen der Faktoren geschrieben werden kann. Allgemein gesagt wird aus log(u*v) nun log(u)+log(v). Angewendet auf die Likelihoodfunktion wird aus dem Logarithmus des Produktes der Einzelwahrscheinlichkeiten log(∏P(di|p,b)) nun die Summe:
kkk Die Ermittlung der Fehleroberfläche mittels der MLE wird in der R-Shiny-App "Fitting" veranschaulicht.