Faktorenanalyse und Rotationsverfahren: Unterschied zwischen den Versionen
Wehner (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
Elisa (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
||
| Zeile 17: | Zeile 17: | ||
[[File:4_2_FA_3.PNG|600px|Abbildung 2: Faktorladungen von 12 Variablen vor (links) bzw. nach (rechts) Varimax-Rotation]] | [[File:4_2_FA_3.PNG|600px|Abbildung 2: Faktorladungen von 12 Variablen vor (links) bzw. nach (rechts) Varimax-Rotation|link=Ausgelagerte_Bildbeschreibungen#Varimax-Rotation|Ausgelagerte Bildbeschreibung von Varimax-Rotation]] | ||
Version vom 13. Dezember 2021, 22:30 Uhr
Das Ziel einer Faktorenanalyse ist in einem Datensatz Faktoren zu identifizieren, mit welchen die Beziehungen zwischen den vielen erfassten Variablen möglichst gut erklärt werden können. Die Durchführung einer Hauptkomponentenanalyse führt zur Ermittlung von ebenso vielen Hauptkomponenten, wie Variablen in die Analyse einbezogen werden. Im Zuge der mit einer Faktorenanalyse in der Regel angestrebten Ziele einer Dimensionsreduzierung und der Bildung inhaltlich gut interpretierbarer Faktoren, ist eine Beschränkung auf wenige Faktoren anzustreben, die einen hohen Anteil der Varianz der Variablen erklären.
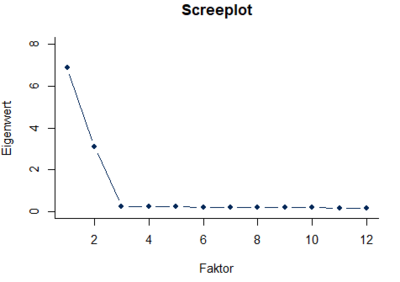
Grundlage für die Entscheidung über die Zahl der in den weiteren Analyseschritten zu berücksichtigenden Faktoren bilden die Eigenwerte, d.h. die Varianzaufklärung der einzelnen Variablen. Die Eigenwerte werden grafisch im sogenannten Scree-Plot dargestellt. In vielen Fällen liefert bereits die visuelle Inspektion des Scree-Plots hinreichende Hinweise über die sinnvolle Zahl zu berücksichtigender Faktoren. Das ist insbesondere dann der Fall, wenn der Screeplot einen Knick aufweist (Abbildung 1). In diesen Fällen ergibt sich die Anzahl der zu berücksichtigenden Faktoren aus der Anzahl der Eigenwerte vor dem Knick. Im Beispiel ergibt sich demnach, dass zwei Faktoren für die weitere Analyse ausgewählt werden sollten.
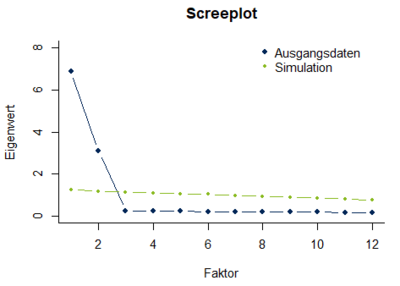
Sehr unterstützend kann die Methode der Parallelanalyse bei der Bestimmung der Faktorenzahl sein. Dabei werden im Beispiel aus Abbildung 1 zwölf Zufallsvariablen gebildet, die identisch normalverteilt sind und in der Population unkorreliert sind. Die Zahl der Werte der Zufallsvariablen entspricht dem Stichprobenumfang im Beispiel. Die Korrelationen zwischen den Zufallsvariablen beim gegebenen Stichprobenumfang kommen lediglich zufällig zustande. Bei der Parallelanalyse werden die Eigenwerte der so erzeugten Hauptkomponenten den Eigenwerten aus den Daten der Stichprobe gegenübergestellt (Abbildung 2). Diejenigen Faktoren, deren Eigenwerte größer sind als die Eigenwerte der Zufallsvariablen, werden für die weitere Analyse ausgewählt. Im Beispiel ergibt sich im Ergebnis der Parallelanalyse, dass zwei Faktoren für die weitere Analyse ausgewählt werden sollten. Das Ergebnis entspricht dem Ergebnis nach der visuellen Analyse des Scree-Plots.
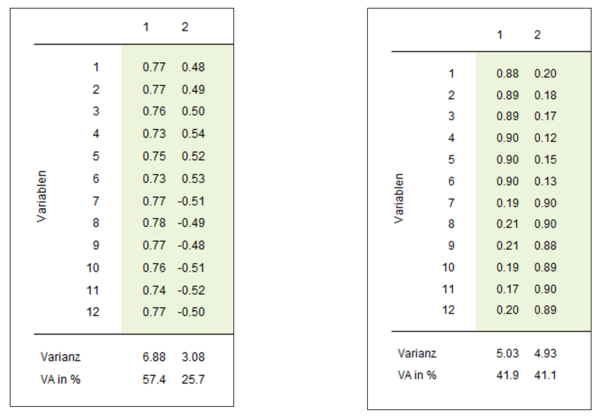
Ein weniger zu empfehlendes Kriterium ist das Kaiser-Gutmann-Kriterium, nach dem alle Faktoren mit Eigenwerten größer als Eins weiterverwendet werden sollen. Nach diesem Kriterium würde sich zwar im Beispiel ebenfalls die Zahl von zwei Faktoren ergeben, allgemein werden nach diesem Kriterium jedoch zu viele Faktoren weiterverwendet. Nach der Entscheidung für zwei Faktoren, mit denen im Beispiel mehr als 80% der Varianz der zwölf Variablen aufgeklärt werden können, können Rotationsmethoden angewendet werden, um eine gute Zuordnung der Variablen zu den Faktoren zu erzielen. Eine wichtige orthogonale Rotationsmethode besteht in der Varimax-Rotation, bei der die Varianz der quadrierten Faktorladungen maximiert wird. Das Ergebnis ist in Abbildung 3 dargestellt, in der die Ladungen der beiden Faktoren vor und nach der Varimax-Rotation gegenübergestellt werden.
Aus Abbildung 3 wird deutlich, dass die Zuordnung der Variablen nach der Varimax-Rotation eindeutiger möglich ist als vorher. Die gesamte Varianzaufklärung der zwölf Variablen im Beispiel durch die beiden Faktoren hat sich nicht verändert, allerdings gab es Verschiebungen zwischen den beiden Faktoren. Die Kommunalitäten der Variablen (Summe der quadrierten Faktorladungen einer Variablen über beide Faktoren) sind ebenfalls unverändert. Um eine noch eindeutigere Zuordnung von Variablen zu Faktoren zu erzielen, können neben orthogonalen auch schiefwinklige Rotationsverfahren eingesetzt werden.
kkk Im Video werden die Prinzipien der Faktorenanalyse und der Rotationsverfahren näher erläutert.
kkk In der interaktiven Simulation lassen sich die Methoden zur Bestimmung der Faktorenanzahl sowie Rotationsverfahren im Rahmen der Faktorenanalyse nachvollziehen.
Weiterführende Literatur
Bortz, J., & Schuster, C. (2016). Statistik für Human- und Sozialwissenschaftler. Berlin: Springer.
Bühner, M. (2010). Einführung in die Test- und Fragebogenkonstruktion (3. Aufl.; Kapitel 6). München: Pearson Studium.
Eid, M., Gollwitzer, M., & Schmitt, M. (2017). Statistik und Forschungsmethoden. Weinheim: Beltz.
Rudolf, M. & Buse, J. (2020). Multivariate Verfahren. Eine praxisorientierte Einführung mit Anwendungsbeispielen (3. Aufl., Kapitel 9.3 und 9.4). Göttingen: Hogrefe.