Sequential Sampling Modelle

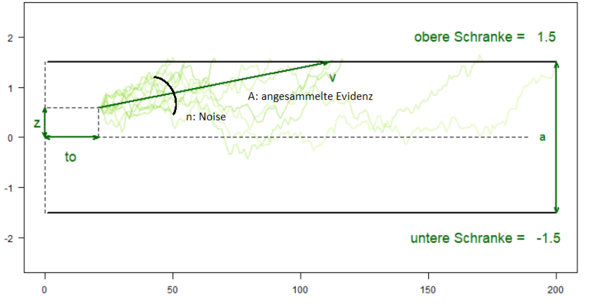
Sequential Sampling Modelle stellen einfache „psychologische“ Modelle zur Simulation von Entscheidungsprozessen dar, welche die Ansammlung von Evidenz über mehrere Zeitschritte bis zum Erreichen einer Entscheidungsschwelle, welche das Ausführen einer Reaktion zur Folge hat, beschreiben. Sie basieren auf der Grundannahme, dass Menschen Entscheidungen treffen, indem sie nach und nach Informationen sammeln, bis eine bestimmte Schwelle erreicht ist. Die Akkumulation von Informationen findet dabei nicht strikt linear statt, sondern ist von Rauschen überlagert.

Sequential Sampling Modelle sind probabilistische Modelle, weshalb deren Output auch dann variieren kann, wenn das System mehrmals mit dem gleichen Input ausgeführt wird. Den Gegenpart dazu stellen deterministische Modelle dar, die sich dadurch auszeichnen, dass sich der Output bei gleichem Input nicht unterscheidet. Theoretiker betrachten probabilistische im Vergleich zu deterministischen Modellen als die besseren Beschreibungen für Befunde aus der Neurowissenschaft und Psychologie, da sie deren Messwerte, welche auch bei einfachsten Aufgaben viele Variationen beinhalten, akkurater reflektieren.

Ein Sequential Sampling lässt sich vereinfacht durch die folgende Formel beschreiben:

x(t) … Entscheidungszustand zum Zeitpunkt t

A … Evidenz (positiv / negativ)

n … Noise (Rauschen / Fehler)

Grundlage des Modells bildet eine Entscheidungsvariable x, welche den aktuellen Systemzustand wiederspiegelt und somit die bis zu einem Zeitpunkt angesammelte Evidenz für eine Option erfasst. Während des Prozesses der Entscheidungsfindung werden unter mehr oder weniger stark vorhandenem Rauschen zunehmend Informationen gesammelt, welche die Entscheidungsvariable stärker in Richtung einer der beiden Antworten bewegen. Sobald x eine der Schranken (= threshold) überschritten hat, wird die Entscheidung getroffen und der Evidenzakkumulationsprozess ist für diesen Durchlauf beendet.

Das am häufigsten verwendete Sequential Sampling Modell ist das Drift Diffusion Modell, dessen Evidenzakkumulationsprozess von mehreren Parametern beeinflusst wird, welche im Folgenden vorgestellt werden.

Modellparameter des Drift Diffusion Modells

Verschiedene Modellparameter haben Einfluss auf die Ergebnisse des modellierten Evidenzakkumulationsprozesses. Die am häufigsten verwendeten Parameter stellen der Driftparameter v, der Schrankenabstand a, der Entscheidungsbias z, und die non-decision time to dar.

• Driftrate v

Die Driftrate des Modells repräsentiert die mittlere Geschwindigkeit der Evidenzverarbeitung (Information pro Zeiteinheit) bzw. wie schnell sich der Akkumulationsprozess pro Zeiteinheit einer bestimmten Schwelle annähert. Eine positive Driftrate besagt, dass die Informationen für Option 1 schneller kodiert werden. Eine negative Driftrate zeigt, dass die Informationen für Option 2 schneller kodiert werden.

• Schrankenabstand a

Eine Entscheidungsreaktion entsteht durch das Überschreiten einer festen Grenze der angesammelten Evidenz für eine Option. Liegen die Schranken eng beieinander, reichen wenige (zufällige) Einflüsse aus, um eine Entscheidung zu treffen. Sind sie weiter voneinander entfernt, wird mehr Evidenz benötigt. Damit soll im Modell der Fall simuliert werden, dass Probanden versuchen Fehler zu vermeiden und eine sichere Entscheidung treffen möchten.

• Entscheidungsbias z

Der Bias z, welcher die Antworttendenz beschreibt, ergibt sich aus dem Verhältnis des Startwertes von x zur Position der Schranken. Er beschreibt, ob durch Priming o.ä. bereits zu Trialbeginn eine Antworttendenz in eine Richtung vorliegt.

• Non-decision time to

Die non-decision time to repräsentiert Prozesse, die während einer Entscheidung stattfinden, aber nicht zum eigentlichen Entscheidungsprozess gehören (sogenannte non-decisional processes), wie beispielsweise die Zeit für die motorische Ausführung einer Reaktion. Die geschätzte Dauer dieser Prozesse wird zur eigentlichen Zeit des Entscheidungsprozesses addiert und führt somit zu einer Verschiebung der Reaktionszeitverteilung.

Betrachtet man verschiedene Drift Diffusion Modelle findet sich teilweise zudem die Angabe weiterer Parameter. Das Diffusionsmodell (fast-dm) von Voss, Rothermund, Gast und Wentura (2013) postuliert beispielsweise einen zusätzlichen Parameter d, welcher einen Offset zwischen to für die untere und to für die obere Option beschreibt. Dies geht auf den Effekt zurück, dass fehlerhafte Entscheidungen häufig impulsiver getroffen werden als korrekte Antworten.

kkk Die eigenständige Exploration der Parametereinflüsse dieses Modells ist zudem im Rahmen der Simulation Statistische Modelle möglich.

Modell ohne Evidenz

In Situationen, in denen keine Evidenz für eine der beiden Optionen vorhanden ist, spiegelt der Evidenzakkumulationsprozess nur zufälliges normalverteiltes Rauschen wieder, welches aber im Laufe der Zeit trotzdem zum Überschreiten einer Schwelle und somit einer Antwortreaktion führt.

Bildet man zu jedem Zeitschritt den Durchschnitt der Werte aller Random Walks (= Darstellungen der Evidenzakkumulation während eines einzelnen Trials), so entsprechen diese Durchschnittswerte für v = 0 dem Startwert des Entscheidungszustands. Die Varianz zwischen den Random Walks erhöht sich jedoch mit jedem weiteren Zeitschritt.

Vorteile und Anwendung

Durch die Betrachtung einer ausreichend großen Menge an Trials erlaubt das Drift Diffusion Modell die Darstellung und Modellierung einer gut fittenden Reaktionszeitverteilung mit differenzierten Parametern. Damit ist die Modellierung des zeitlichen Ablaufs der Entscheidungsfindung möglich.

Es wird zudem zur Untersuchung von Bedingungs- und Gruppenunterschieden sowie in der weiterführenden Datenanalyse verwendet.

Eine damit zu untersuchende Fragestellung könnte beispielsweise lauten: „Treffen alte Menschen Entscheidungen langsamer als jüngere Personen oder sind sie nur vorsichtiger in ihrer Wahl?“ Lassen sich die Unterschiede der Reaktionszeitverteilungen zwischen beiden Gruppen stärker durch einen unterschiedlichen Drift v erklären, ist es wahrscheinlicher, dass die Informationsaufnahmegeschwindigkeit jüngerer Menschen höher ist als die der älteren Probanden. Eine bessere Erklärung der unterschiedlichen Verteilungen durch verschiedene Schrankenabstände liefert hingegen Evidenz dafür, dass ältere Menschen mehr Evidenz für die Wahl einer Entscheidung benötigen und somit vorsichtiger sind. Eine ähnliche Fragestellung untersuchte beispielsweise die Studie von Ratcliff et al. (2000), welche für ältere Probanden höhere to Werte fand.