Multikollinearität: Unterschied zwischen den Versionen
Wehner (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
Wehner (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
{{Nav|Navigation|Statistik_MV|Hauptseite}} | {{Nav|Navigation|Statistik_MV|Hauptseite}} | ||
Das Ziel der [[Grundlagen der multiplen linearen Regression|multiplen Regressionsanalyse]] besteht darin, ein möglichst genaues Modell zur Vorhersage eines Kriteriums aus einer gegebenen Anzahl an Prädiktoren zu schätzen und dabei den Einfluss von Störvariablen zu kontrollieren. Ein häufiger Grund für unpräzise Parameterschätzungen in multiplen Regressionen ist Multikollinearität. Multikollinearität bezeichnet dabei die wechselseitige Abhängigkeit von Variablen in multivariaten Analysen. | |||
Um die Regressionskoeffizienten einer multiplen linearen Regression interpretieren zu können, ist es wichtig, sich die Korrelationen zwischen den Variablen anschauen. Sind die Ergebnisse der Korrelationsanalyse und der Regressionsanalyse analog, d.h. hohe und signifikante Korrelationskoeffizienten zwischen Prädiktoren und Kriterium entsprechen hohen und signifikanten Regressionskoeffizienten, kann von einer präzisen Parameterschätzung ausgegangen werden. Korrelationen der Prädiktoren mit dem Kriterium, die sich nicht in der Regressionsanalyse widerspiegeln sind Hinweise auf Multikollinearität und sollten weitergehend untersucht werden. Multikollinearität entsteht, wenn die Prädiktoren eines Modelles untereinander korrelieren. Typische Formen der Multikollinearität sind Redundanz und Suppression. | |||
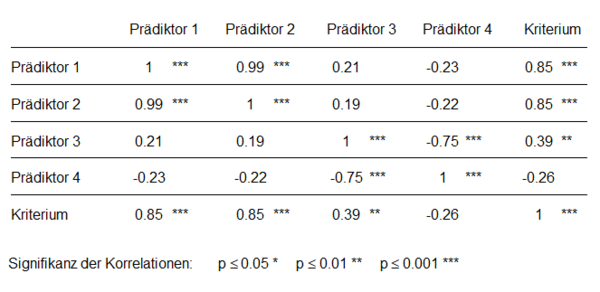
Redundanz tritt auf, wenn ein Prädiktor den Vorhersagewert eines zweiten Prädiktors übernimmt. Trotz signifikanter Korrelation mit dem Kriterium leisten redundante Prädiktoren im Regressionsmodell keinen signifikanten Beitrag zur Varianzaufklärung des Kriteriums. In Abbildung 1 sieht man, dass Prädiktor 1 und Prädiktor 2 hoch und signifikant mit dem Kriterium korrelieren (r = 0.85). | |||
[[File:3_4_MLR_MK_1.PNG|600px|Abbildung 1: Korrelationsmatrix einer multiplen linearen Regression mit 4 Prädiktoren]] | |||
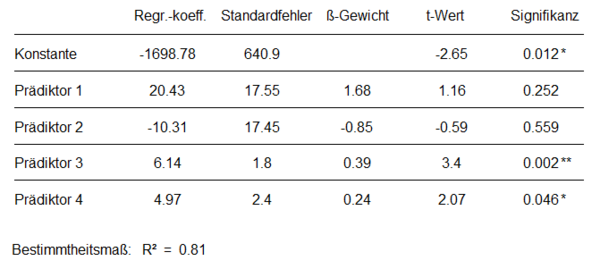
In der Regressionsanalyse hat jedoch keiner der beiden Prädiktoren einen signifikanten Einfluss auf das Kriterium (Abbildung 2). | |||
[[File:3_4_MLR_MK_2.PNG|600px|Abbildung 2: Ergebnisse der multiplen linearen Regression mit den Prädiktoren aus Abbildung 1]] | |||
Die sehr hohe Korrelation der beiden Prädiktoren von r = 0.99 ist ein starker Hinweis auf Redundanz. Die Prädiktoren sind fast identisch und klären somit fast die gleichen Varianzanteile des Kriteriums auf. Entfernt man einen der beiden Prädiktoren aus der Analyse, leistet der verbliebene Prädiktor plötzlich einen signifikanten Beitrag zur Vorhersage des Kriteriums. Einer der beiden Prädiktoren ist also redundant und sollte aus der Analyse entfernt werden. Welcher der beiden Prädiktoren entbehrlicher ist, lässt sich mithilfe von [[Merkmalsselektionsverfahren]] feststellen. | |||
Suppression liegt vor, wenn ein Prädiktor unerwünschte Varianzanteile anderer Prädiktoren unterdrückt und dadurch diese Prädiktoren in der Regressionsanalyse stärker zur Vorhersage beitragen, als es die Korrelation mit dem Kriterium vermuten lässt. Eine Suppressorvariable korreliert, anders als eine redundante Variable, nicht bzw. nur gering mit dem Kriterium, aber ebenfalls mit anderen Prädiktoren. Es sind also hauptsächlich die Varianzanteile der Prädiktoren korreliert, die nicht zur Vorhersage des Kriteriums beitragen. Diese korrelierten Störanteile werden bei der Schätzung der Regressionskoeffizienten entfernt bzw. unterdrückt, was in dem Modell zur Verbesserung des Vorhersagebeitrags der beteiligten Prädiktoren führen kann. In den Abbildungen 1 und 2 wird Suppression anhand der Prädiktoren 3 und 4 veranschaulicht. Prädiktor 4 hat in der Korrelationsanalyse eine nichtsignifikante, negative Korrelation von r = -0.26 mit dem Kriterium, zeigt in der Regressionsanalyse jedoch einen signifikant von 0 verschiedenen positiven Regressionskoeffizienten (β = 0.24). Die signifikante Korrelation mit Prädiktor 3 (r = -0.75) ist ein Hinweis auf Multikollinearität. Entfernt man Prädiktor 4 aus dem Modell, sinkt das Bestimmtheitsmaß um 0.02. Außerdem wird das Beta-Gewicht von Prädiktor 3 geringer und der dazugehörige p-Wert höher. Entfernt man Prädiktor 3 aus der Analyse, verschwindet der Einfluss von Prädiktor 4 auf das Kriterium. Prädiktor 4 hat – wie die Korrelationsanalyse vermuten lässt – nur im Zusammenhang mit Prädiktor 3 eine entscheidende Rolle im Regressionsmodell. Es handelt sich also um einen Suppressionseffekt mit Prädiktor 4 als Suppressorvariable. | |||
Neben dem Betrachten der Korrelationsanalysen und dem Vergleich mit den Ergebnissen der Regressionsanalysen können Multikollinearitätsmaße auch rechnerisch bestimmt werden. Die Toleranz stellt eine Möglichkeit zur Bestimmung von Multikolliniarität dar. Zur Berechnung subtrahiert man das multiple Bestimmtheitsmaß R² einer multiplen Regression, mit dem ein Prädiktor j durch alle anderen Prädiktoren vorhergesagt wird, von 1 (Tol<sub>j</sub> = 1 - R²). Ist R² hoch, spricht das für einen hohen Zusammenhang der Prädiktoren und somit für das Vorliegen von Multikollinearität. Da aus hohen Bestimmtheitsmaßen niedrige Toleranzwerte Tol<sub>j</sub> resultieren, sind niedrige Werte der Toleranz ein Hinweis auf Multikollinearität in den Daten. Die Werte der Toleranz befinden sich wie R² im Wertebereich zwischen 0 und 1. Im vorliegenden Beispiel weisen die kleinen Toleranzwerte aller Prädiktoren auf Multikollinearitäten hin. Für Prädiktor 1 und 2 ergeben sich sogar Toleranzwerte von 0, da sie fast perfekt durch den jeweils anderen Prädiktor vorhersagbar sind. | |||
Ein weiteres Maß zur Bestimmung der Multikollinearität ist der Varianzinflationsfaktor (VIF). Dieser berechnet sich als Kehrwert der Toleranz: | |||
[[File:3_4_MLR_MK_Formel.PNG|160px]] | |||
Die Untergrenze des VIFs ist 1 und gibt an, dass der jeweilige Prädiktor j unkorreliert mit allen anderen Prädiktoren ist. Ein höherer VIF bedeutet dementsprechend größere Multikollinearität. | |||
[[Datei:Videolink_neu.PNG|link=http://141.76.19.82:3838/mediawiki/konfidenzintervall_link.html | [[Datei:Videolink_neu.PNG|link=http://141.76.19.82:3838/mediawiki/konfidenzintervall_link.html | ||
|120px]] <span style="color: white"> kkk </span> Im [http://141.76.19.82:3838/mediawiki/pwertlink.html Video] wird | |120px]] <span style="color: white"> kkk </span> Im [http://141.76.19.82:3838/mediawiki/pwertlink.html Video] wird das Auftreten von Multikollinearität im Rahmen multipler linearer Regressionen näher erläutert. | ||
[[Datei:Simulationslink_neu2.PNG|link=http://141.76.19.82:3838/mediawiki/1_1_p-Wert/App_Version/ | [[Datei:Simulationslink_neu2.PNG|link=http://141.76.19.82:3838/mediawiki/1_1_p-Wert/App_Version/ | ||
|120px]] <span style="color: white"> kkk </span> | |120px]] <span style="color: white"> kkk </span> In der [http://141.76.19.82:3838/mediawiki/1_1_p-Wert/App_Version/ interaktiven Simulation] können Redundanz- und Suppressionseffekte anhand von verschiedenen Beispieldatensätzen nachvollzogen werden. | ||
| Zeile 34: | Zeile 44: | ||
'''''Weiterführende Literatur''''' | '''''Weiterführende Literatur''''' | ||
Rudolf, M., & Kuhlisch, W. (2008). ''Biostatistik: Eine Einführung für Biowissenschaftler'' (Kapitel 7. | Bortz, J., & Schuster, C. (2017). ''Statistik für Human- und Sozialwissenschaftler''. Springer-Verlag. | ||
Eid, M., Gollwitzer, M., & Schmitt, M. (2017). ''Statistik und Forschungsmethoden''. Beltz. | |||
Rudolf, M. & Buse, J. (2020). ''Multivariate Verfahren. Eine praxisorientierte Einführung mit Anwendungsbeispielen'' (3. Aufl., Kapitel 2.2 und 2.3). Göttingen: Hogrefe. | |||
Rudolf, M., & Kuhlisch, W. (2008). ''Biostatistik: Eine Einführung für Biowissenschaftler'' (Kapitel 7.6). München: Pearson Studium. | |||
Version vom 10. März 2020, 22:48 Uhr
Das Ziel der multiplen Regressionsanalyse besteht darin, ein möglichst genaues Modell zur Vorhersage eines Kriteriums aus einer gegebenen Anzahl an Prädiktoren zu schätzen und dabei den Einfluss von Störvariablen zu kontrollieren. Ein häufiger Grund für unpräzise Parameterschätzungen in multiplen Regressionen ist Multikollinearität. Multikollinearität bezeichnet dabei die wechselseitige Abhängigkeit von Variablen in multivariaten Analysen.
Um die Regressionskoeffizienten einer multiplen linearen Regression interpretieren zu können, ist es wichtig, sich die Korrelationen zwischen den Variablen anschauen. Sind die Ergebnisse der Korrelationsanalyse und der Regressionsanalyse analog, d.h. hohe und signifikante Korrelationskoeffizienten zwischen Prädiktoren und Kriterium entsprechen hohen und signifikanten Regressionskoeffizienten, kann von einer präzisen Parameterschätzung ausgegangen werden. Korrelationen der Prädiktoren mit dem Kriterium, die sich nicht in der Regressionsanalyse widerspiegeln sind Hinweise auf Multikollinearität und sollten weitergehend untersucht werden. Multikollinearität entsteht, wenn die Prädiktoren eines Modelles untereinander korrelieren. Typische Formen der Multikollinearität sind Redundanz und Suppression.
Redundanz tritt auf, wenn ein Prädiktor den Vorhersagewert eines zweiten Prädiktors übernimmt. Trotz signifikanter Korrelation mit dem Kriterium leisten redundante Prädiktoren im Regressionsmodell keinen signifikanten Beitrag zur Varianzaufklärung des Kriteriums. In Abbildung 1 sieht man, dass Prädiktor 1 und Prädiktor 2 hoch und signifikant mit dem Kriterium korrelieren (r = 0.85).
In der Regressionsanalyse hat jedoch keiner der beiden Prädiktoren einen signifikanten Einfluss auf das Kriterium (Abbildung 2).
Die sehr hohe Korrelation der beiden Prädiktoren von r = 0.99 ist ein starker Hinweis auf Redundanz. Die Prädiktoren sind fast identisch und klären somit fast die gleichen Varianzanteile des Kriteriums auf. Entfernt man einen der beiden Prädiktoren aus der Analyse, leistet der verbliebene Prädiktor plötzlich einen signifikanten Beitrag zur Vorhersage des Kriteriums. Einer der beiden Prädiktoren ist also redundant und sollte aus der Analyse entfernt werden. Welcher der beiden Prädiktoren entbehrlicher ist, lässt sich mithilfe von Merkmalsselektionsverfahren feststellen.
Suppression liegt vor, wenn ein Prädiktor unerwünschte Varianzanteile anderer Prädiktoren unterdrückt und dadurch diese Prädiktoren in der Regressionsanalyse stärker zur Vorhersage beitragen, als es die Korrelation mit dem Kriterium vermuten lässt. Eine Suppressorvariable korreliert, anders als eine redundante Variable, nicht bzw. nur gering mit dem Kriterium, aber ebenfalls mit anderen Prädiktoren. Es sind also hauptsächlich die Varianzanteile der Prädiktoren korreliert, die nicht zur Vorhersage des Kriteriums beitragen. Diese korrelierten Störanteile werden bei der Schätzung der Regressionskoeffizienten entfernt bzw. unterdrückt, was in dem Modell zur Verbesserung des Vorhersagebeitrags der beteiligten Prädiktoren führen kann. In den Abbildungen 1 und 2 wird Suppression anhand der Prädiktoren 3 und 4 veranschaulicht. Prädiktor 4 hat in der Korrelationsanalyse eine nichtsignifikante, negative Korrelation von r = -0.26 mit dem Kriterium, zeigt in der Regressionsanalyse jedoch einen signifikant von 0 verschiedenen positiven Regressionskoeffizienten (β = 0.24). Die signifikante Korrelation mit Prädiktor 3 (r = -0.75) ist ein Hinweis auf Multikollinearität. Entfernt man Prädiktor 4 aus dem Modell, sinkt das Bestimmtheitsmaß um 0.02. Außerdem wird das Beta-Gewicht von Prädiktor 3 geringer und der dazugehörige p-Wert höher. Entfernt man Prädiktor 3 aus der Analyse, verschwindet der Einfluss von Prädiktor 4 auf das Kriterium. Prädiktor 4 hat – wie die Korrelationsanalyse vermuten lässt – nur im Zusammenhang mit Prädiktor 3 eine entscheidende Rolle im Regressionsmodell. Es handelt sich also um einen Suppressionseffekt mit Prädiktor 4 als Suppressorvariable.
Neben dem Betrachten der Korrelationsanalysen und dem Vergleich mit den Ergebnissen der Regressionsanalysen können Multikollinearitätsmaße auch rechnerisch bestimmt werden. Die Toleranz stellt eine Möglichkeit zur Bestimmung von Multikolliniarität dar. Zur Berechnung subtrahiert man das multiple Bestimmtheitsmaß R² einer multiplen Regression, mit dem ein Prädiktor j durch alle anderen Prädiktoren vorhergesagt wird, von 1 (Tolj = 1 - R²). Ist R² hoch, spricht das für einen hohen Zusammenhang der Prädiktoren und somit für das Vorliegen von Multikollinearität. Da aus hohen Bestimmtheitsmaßen niedrige Toleranzwerte Tolj resultieren, sind niedrige Werte der Toleranz ein Hinweis auf Multikollinearität in den Daten. Die Werte der Toleranz befinden sich wie R² im Wertebereich zwischen 0 und 1. Im vorliegenden Beispiel weisen die kleinen Toleranzwerte aller Prädiktoren auf Multikollinearitäten hin. Für Prädiktor 1 und 2 ergeben sich sogar Toleranzwerte von 0, da sie fast perfekt durch den jeweils anderen Prädiktor vorhersagbar sind.
Ein weiteres Maß zur Bestimmung der Multikollinearität ist der Varianzinflationsfaktor (VIF). Dieser berechnet sich als Kehrwert der Toleranz:
Die Untergrenze des VIFs ist 1 und gibt an, dass der jeweilige Prädiktor j unkorreliert mit allen anderen Prädiktoren ist. Ein höherer VIF bedeutet dementsprechend größere Multikollinearität.
kkk Im Video wird das Auftreten von Multikollinearität im Rahmen multipler linearer Regressionen näher erläutert.
kkk In der interaktiven Simulation können Redundanz- und Suppressionseffekte anhand von verschiedenen Beispieldatensätzen nachvollzogen werden.
Weiterführende Literatur
Bortz, J., & Schuster, C. (2017). Statistik für Human- und Sozialwissenschaftler. Springer-Verlag.
Eid, M., Gollwitzer, M., & Schmitt, M. (2017). Statistik und Forschungsmethoden. Beltz.
Rudolf, M. & Buse, J. (2020). Multivariate Verfahren. Eine praxisorientierte Einführung mit Anwendungsbeispielen (3. Aufl., Kapitel 2.2 und 2.3). Göttingen: Hogrefe.
Rudolf, M., & Kuhlisch, W. (2008). Biostatistik: Eine Einführung für Biowissenschaftler (Kapitel 7.6). München: Pearson Studium.