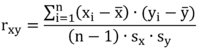Einfache lineare Korrelation
Über verschiedene Korrelationsanalyseverfahren lässt sich ermitteln, ob bzw. in welchem Ausmaß zwei Variablen bzw. Merkmale zusammenhängen. Besonders lineare Zusammenhänge spielen in der Praxis eine wichtige Rolle und sollen im Folgenden behandelt werden.
Der lineare Zusammenhang zweier metrischer Variablen lässt sich über Pearsons Produkt-Moment-Korrelationskoeffizienten r bestimmen. Dieser wird aus den Daten einer Stichprobe geschätzt und lässt sich folgendermaßen darstellen:
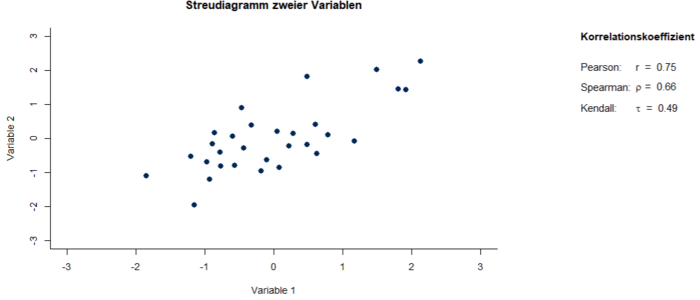
xi und yi sind einzelne Messwerte der Variablen, von denen jeweils der arithmetische Mittelwert der jeweiligen Variable abgezogen wird. Werden die Messwertpaare miteinander multipliziert, diese Produkte summiert und die Summe anschließend durch (n-1) geteilt, ergibt sich die Kovarianz. Um Schlüsse über die vorliegende Stichprobe zu ziehen, würde man hier durch n teilen. Für inferenzstatistische Schlüsse, die über die Stichprobe hinaus verallgemeinert werden können, muss jedoch durch (n-1) geteilt werden. Die Kovarianz gibt an, wie hoch die gemeinsame Variation der Merkmale um die jeweiligen Mittelwerte ist. Normiert man diese noch an den Standardabweichungen sx und sy , erhält man Pearson’s r als Maß für die Korrelation. Diese kann nur Werte zwischen -1 und 1 annehmen und beschreibt die Stärke des Zusammenhangs zweier Variablen. Der Wert von 1 beschreibt einen streng positiven linearen Zusammenhang und der Wert -1 einen streng negativen linearen Zusammenhang. Ein Wert von 0 macht deutlich, dass zwischen den beiden Variablen kein linearer Zusammenhang besteht. In Abbildung 1 ist der Zusammenhang zweier Variablen in einem Streudiagramm grafisch veranschaulicht.
Bei Berechnung des Produkt-Moment-Korrelationskoeffizienten ergibt sich ein starker Zusammenhang von r = 0.75.
Der Produkt-Moment-Korrelationskoeffizienten nach Pearson sollte nur angewandt und interpretiert werden, wenn beide Variablen normalverteilt sind und linear zusammenhängen. Liegen ordinalskalierte Daten oder monotone, aber nichtlineare Zusammenhänge vor, ist z.B. der Rangkorrelationskoeffizient nach Spearman die bessere Wahl. Dieser berechnet sich nach dem gleichen Prinzip wie der Korrelationskoeffizient nach Pearson. Dadurch, dass kein metrisches Datenniveau vorausgesetzt wird, müssen zunächst die Messwerte der beiden Variablen in Rangplätze überführt werden. Die Vergabe der Rangplätze kann z.B. in Rudolf & Kuhlisch (2008) nachvollzogen werden. Anschließend kann man Spearmans Rangkorrelationskoeffizient mit der folgenden Formel berechnen:
Diese entspricht weitestgehend der Formel für den Koeffizienten nach Pearson. Nur werden hier nicht die einzelnen Messwerte zur Berechnung genommen, sondern die Rangplätze r der Messwerte und in der Konsequenz auch die arithmetischen Mittelwerte und Standardabweichungen dieser Rangplätze. Auch der Wertebereich des Rangkorrelationskoeffizienten befindet sich zwischen -1 und 1. In Abbildung 1 kann man feststellen, dass Spearmans Rangkorrelationskoeffizient bei den gleichen Daten mit ρ = 0.66 etwas geringer ausfällt als 0.75.
Da der Rangkorrelationskoeffizient nach Spearman die Korrelation nach ähnlichem Prinzip berechnet wie der Produkt-Moment-Korrelationskoeffizient, werden die Rangplätze wie metrische Daten behandelt. D.h. es werden gleiche Abstände zwischen den einzelnen Plätzen angenommen. Ist diese Annahme nicht gegeben, kann stattdessen der Rangkorrelationskoeffizient Kendalls Tau angewendet werden. Dieser vergleicht die Ränge der beiden Variablen paarweise für alle Objekte n. Unterscheiden sich die Rangplätze der beiden Variablen für beide Objekte (z.B. xi > xy und yi > yi ) in die gleiche Richtung handelt es sich um ein konkordantes Paar. Zeigen diese Vergleiche in unterschiedliche Richtungen (z.B. xi > xj und yi < xj ) handelt es sich um ein diskordantes Paar. Nachdem jedes Objektpaar auf Konkordanz überprüft wurde, wird Kendalls Tau mithilfe der folgenden Formel berechnet:
S stellt dabei die Differenz zwischen der Anzahl konkordanter und diskordanter Paare dar. Der Wertebereich von Kendalls Tau befindet sich ebenfalls zwischen -1 und 1. Für den Beispieldatensatz in Abbildung 1 beträgt Kendalls Tau τ = 0.49. Zusätzlich zu der möglichen Anwendung bei ordinalen Daten sind Spearmans ρ und Kendalls τ aufgrund der Verwendung von Rangplätzen weniger anfällig für Ausreißer und Extremwerte auch bei metrischen Merkmalen im Vergleich zu Pearsons r. Für ein tiefer gehendes Verständnis der einfachen linearen Korrelation sei auf die weiterführende Literatur verwiesen.
kkk Im Video werden die Grundlagen der einfachen linearen Korrelation nochmals erläutert.
kkk Wie Streudiagramme verschiedener Korrelationen aussehen und wie sich die beschriebenen Korrelationskoeffizienten beeinflussen lassen, lässt sich in der interaktiven Simulation nachvollziehen.
Weiterführende Literatur
Clauß, G., Finze, F. R., & Partzsch, L. (2011). Grundlagen der Statistik für Soziologen, Pädagogen, Psychologen und Mediziner. Frankfurt: Europa-Lehrmittel
Holling, H. & Gediga, G. (2010). Statistik - Deskriptive Verfahren. Göttingen: Hogrefe.
Rudolf, M., & Kuhlisch, W. (2008). Biostatistik: Eine Einführung für Biowissenschaftler (Kapitel 7.1 und 7.2). München: Pearson Studium.