Hierarchical Gaussian Filter

Der Hierarchische Gaußfilter (Hierarchical Gaussian Filter, HGF) stellt ein hierarchisches probabilistisches Modell dar. Es ermöglicht beispielsweise die Beschreibung individuellen Lernens oder von Wahrnehmungsprozessen unter expliziter Berücksichtigung verschiedener Formen von Unsicherheit. Diese Unsicherheiten können sowohl eine sich schnell veränderte Umwelt als auch Unsicherheiten in der sensorischen Verarbeitung darstellen.

Viele Wahrnehmungstheorien nehmen an, dass Menschen über ein aktualisierbares Modell ihrer Umwelt verfügen, welches kontinuierlich den zu erwartenden sensorischen Input modelliert (generatives Modell). Probabilistische Theorien wie der HGF beschreiben dabei, wie Individuen trotz verrauschter Prozesse und Unsicherheit, mithilfe der sensorischen Informationen, Wissen über ihre Umwelt erlangen. Ein Agent trifft über eine Sequenz von sensorischen Inputs Schlussfolgerungen über seine Umgebung. Dies geschieht auf Basis einer Hierarchie von unbekannten Umweltzuständen (hidden states). Diese hidden states sind als eine Hierarchie von Gauss’schen Zufallsprozessen bzw. Wahrscheinlichkeitsverteilungen repräsentiert, wobei die höhere Ebene jeweils die Unsicherheit (Varianz) der darunterliegenden Ebene bestimmt. Man setzt voraus, dass mit jedem Zeitschritt ein sequentielles Update der Annahmen des Agenten über diese hidden states im Sinne von neuen posterioren Wahrscheinlichkeitsverteilungen erfolgt. Die Vorstellungen über die angenommenen hidden states entwickeln sich über die Zeit als hierarchisch miteinander verbundene Gaussian Random Walks, so dass jeder hidden state die Schrittweite der Entwicklung (Varianz) des nächsten unterliegenden hidden states bestimmt. Die Kopplung der Ebenen wird zudem von Parametern gesteuert, welche den Einfluss von Unsicherheit auf die Informationsverarbeitung prägen und individuelle Unterschiede im Lern- und Wahrnehmungsverhalten widerspiegeln können.

Das Ziel des Modells besteht verallgemeinert darin, das Lernen eines Agenten über eine kontinuierliche, unsichere und veränderliche Größe X (z.B. eine Zufallsvariable) zu beschreiben. Diese Beschreibung erfolgt zunächst einmal mithilfe eines Random Walks und der folgenden Gleichung:

Der Zeitindex für die Veränderung wird dabei durch k repräsentiert und und ϑ stellen den Mittelwert und die Varianz der Normalverteilung für den Random Walk dar. Die sogenannte volatility von x (= Varianz einer Zeitreihe pro Zeiteinheit) wird in dieser Gleichung durch die positive Konstante ϑ festgelegt. Da es jedoch keinen theoretischen Grund für die Annahme gibt, dass diese volatility konstant ist und um deren Veränderung zu ermöglichen, wird ϑ in der folgenden Formel durch eine positive Funktion f einer zweiten Variable x2 (neben x1) ersetzt:

Man nimmt nun weiter an, dass auch x2 einen eigenen Gaussian Random Walk mit konstanter Varianz ϑ durchführt. Die Gleichung zur Berechnung von x1 lässt sich somit auch auf die Berechnung von x2 übertragen. Auch dessen konstante Varianz ϑ lässt sich durch eine positive Funktion einer weiteren Variable x3 ersetzen:

Diese Aufaddierung von Ebenen der Gaussian Random Walks, welche durch ihre Varianzen gekoppelt sind, kann nun bis zu einer beliebigen Anzahl von n Ebenen fortgesetzt werden.

Auf jeder Ebene ist die Kopplung zur nächsthöheren Ebene i + 1 durch eine positive Funktion gegeben, welche die Varianz (Schrittgröße der Random Walks) repräsentiert:

Auf der höchsten Ebene wird die Varianz durch die positive Konstante ϑ bestimmt:

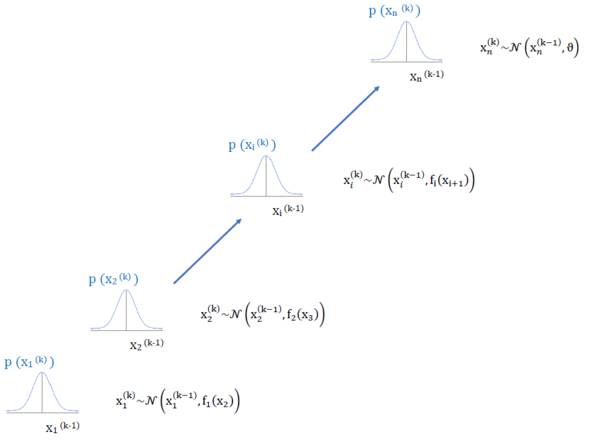
Die folgende Abbildung nach Mathys (2012) fasst die einzelnen Berechnungsschritte nochmals zusammen:

Zur Vervollständigung des Modells ist es zudem nötig fi zu definieren. Flexible Ansätze postulieren, dass jede positive analytische Funktion für fi verwendet werden kann. Einen Überblick über mögliche Funktionen liefert beispielsweise der Artikel von Mathys (2014).

Ein Vorteil des HGF ist, dass die Unsicherheit (volatility) hierarchisch „aufgefangen“ wird. Aufgrund der Kopplung der Ebenen durch hierarchisch miteinander verbundene Gaussian Random Walks wird nicht nur die Unsicherheit der Ergebnisse erfasst, sondern auch deren Unsicherheit und die Unsicherheit der Unsicherheit und so weiter.

Dies ermöglicht unter anderem die Schätzung von durch den Vorgang des sogenannten „filtering“, welcher ebenfalls unter anderem im Artikel von Mathys (2014) näher erläutert wird.