Stichprobenbeschreibung: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „{{Nav|Navigation|Stichproben|Versuchsplanung}} Populationen können mithilfe von Stichproben durch Populationsparameter beschrieben werden. Diese Paramete…“) |
Elisa (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
||
| Zeile 2: | Zeile 2: | ||
[[Populationen]] können mithilfe von Stichproben durch Populationsparameter beschrieben werden. Diese Parameter umfassen beispielsweise Mittelwert und Streuung und werden in der Stichprobe erfasst und dann hochgerechnet, um verallgemeinernde Rückschlüsse auf die Grundgesamtheit (Population) machen zu können: <br/> <br/> | [[Populationen]] können mithilfe von Stichproben durch Populationsparameter beschrieben werden. Diese Parameter umfassen beispielsweise Mittelwert und Streuung und werden in der Stichprobe erfasst und dann hochgerechnet, um verallgemeinernde Rückschlüsse auf die Grundgesamtheit (Population) machen zu können: <br/> <br/> | ||
[[Datei:SP-Beschreibung.png|400px|zentriert]] | [[Datei:SP-Beschreibung.png|400px|zentriert|link=Ausgelagerte_Bildbeschreibungen#Stichprobenbeschreibung|Ausgelagerte Bildbeschreibung von Stichprobenbeschreibung]] | ||
<br/>Solche Rückschlüsse können zwangsläufig nicht komplett akkurat sein, denn die Stichprobe repräsentiert immer nur bedingt die Population. Die Unsicherheit in der Parameterschätzung wird daher z.B. im [[Konfidenzintervall]] angegeben. Je größer jedoch die Stichprobe ist, desto sicherer kann man sich des berechneten Kennwertes sein. Würde die Stichprobe schließlich die gesamte Population umfassen, hätte man maximale Sicherheit erreicht. <br/> <br/> | <br/>Solche Rückschlüsse können zwangsläufig nicht komplett akkurat sein, denn die Stichprobe repräsentiert immer nur bedingt die Population. Die Unsicherheit in der Parameterschätzung wird daher z.B. im [[Konfidenzintervall]] angegeben. Je größer jedoch die Stichprobe ist, desto sicherer kann man sich des berechneten Kennwertes sein. Würde die Stichprobe schließlich die gesamte Population umfassen, hätte man maximale Sicherheit erreicht. <br/> <br/> | ||
Für nähere Ausführungen siehe [[Datenbeschreibung]]. | Für nähere Ausführungen siehe [[Datenbeschreibung]]. | ||
Aktuelle Version vom 13. Dezember 2021, 22:04 Uhr
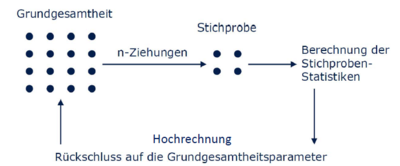
Populationen können mithilfe von Stichproben durch Populationsparameter beschrieben werden. Diese Parameter umfassen beispielsweise Mittelwert und Streuung und werden in der Stichprobe erfasst und dann hochgerechnet, um verallgemeinernde Rückschlüsse auf die Grundgesamtheit (Population) machen zu können:
Solche Rückschlüsse können zwangsläufig nicht komplett akkurat sein, denn die Stichprobe repräsentiert immer nur bedingt die Population. Die Unsicherheit in der Parameterschätzung wird daher z.B. im Konfidenzintervall angegeben. Je größer jedoch die Stichprobe ist, desto sicherer kann man sich des berechneten Kennwertes sein. Würde die Stichprobe schließlich die gesamte Population umfassen, hätte man maximale Sicherheit erreicht.
Für nähere Ausführungen siehe Datenbeschreibung.