Randomisierung: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „{{Nav|Navigation|Max-Kon-Min|Versuchsplanung}} Bei der Randomisierung wird angenommen, dass sich alle bekannten und unbekannten Merkmale der Versuchspersonen,…“) |
Elisa (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
||
| (6 dazwischenliegende Versionen von einem anderen Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Nav|Navigation|Max-Kon-Min|Versuchsplanung}} | {{Nav|Navigation|Max-Kon-Min|Versuchsplanung}} | ||
Bei der Randomisierung wird angenommen, dass sich alle bekannten und unbekannten Merkmale der Versuchspersonen, die in einem Versuch als [[Störvariablen]] wirksam werden könnten, zufällig auf die Versuchbedingungen verteilen (Sarris, 1990). Sie ist eine der [[Kontrollprinzipien|Kontrolltechniken]] zur Kontrolle der [[Sekundärvarianz]] in einem [[Experimente|Experiment]]. | Bei der Randomisierung wird angenommen, dass sich alle bekannten und unbekannten Merkmale der Versuchspersonen, die in einem Versuch als [[Störvariablen]] wirksam werden könnten, zufällig auf die Versuchbedingungen verteilen (Sarris, 1990). Sie ist eine der [[Kontrollprinzipien|Kontrolltechniken]] zur Kontrolle der [[Varianz#Sekundärvarianz|Sekundärvarianz]] in einem [[Experimente|Experiment]]. | ||
Die Randomisierung ist die sogenannte Königsdisziplin unter den Kontrolltechniken und wird mit der Faustregel 3x Zufall beschrieben: Zufällige Auswahl der [[Stichprobe]] aus der Grundgesamtheit (siehe [[Population]]), zufällige Einteilung der Versuchspersonen in die Versuchsgruppen und zufällige Zuteilung der Versuchsgruppen zu den einzelnen Versuchsbedingungen. | Die Randomisierung ist die sogenannte Königsdisziplin unter den Kontrolltechniken und wird mit der Faustregel 3x Zufall beschrieben: Zufällige Auswahl der [[Stichproben|Stichprobe]] aus der Grundgesamtheit (siehe [[Populationen|Population]]), zufällige Einteilung der Versuchspersonen in die Versuchsgruppen und zufällige Zuteilung der Versuchsgruppen zu den einzelnen Versuchsbedingungen. | ||
Es wird davon ausgegangen, dass sich alle unbekannten und bekannten Störvariablen per Zufall auf die verschiedenen Versuchsbedingungen verteilen. Dadurch sind die Gruppen und deren Ausgangswerte vergleichbar. Das Zufallsprinzip kann beispielsweise mit Würfeln oder Zufallszahlentabellen realisiert werden. | Es wird davon ausgegangen, dass sich alle unbekannten und bekannten Störvariablen per Zufall auf die verschiedenen Versuchsbedingungen verteilen. Dadurch sind die Gruppen und deren Ausgangswerte vergleichbar. Das Zufallsprinzip kann beispielsweise mit Würfeln oder Zufallszahlentabellen realisiert werden. | ||
Der große Vorteil des Randomisierungsprinzips ist die Kontrolle auch aller unbekannten Störvariablen. Die Versuchsgruppen unterscheiden sich also vor Versuchsbeginn nicht systematisch. Aus diesem Grund stellt die Randomisierung die ideale Kontrolltechnik zur Kontrolle der Sekundärvarianz dar. In der Praxis ist es häufig schwierig, tatsächlich das Prinzip im Sinne des "3xZufalls" zu realisieren. Stattdessen wird oft auf [[ | Der große Vorteil des Randomisierungsprinzips ist die Kontrolle auch aller unbekannten Störvariablen. Die Versuchsgruppen unterscheiden sich also vor Versuchsbeginn nicht systematisch. Aus diesem Grund stellt die Randomisierung die ideale Kontrolltechnik zur Kontrolle der Sekundärvarianz dar. In der Praxis ist es häufig schwierig, tatsächlich das Prinzip im Sinne des "3xZufalls" zu realisieren. Stattdessen wird oft auf [[Quasi-Experimente|Quasiexperimentelle Pläne]] zurückgegriffen. | ||
Bei der Randomisierung ist es sehr wichtig, dass das Gesetz der großen Zahlen berücksichtigt wird. Dieses besagt, dass für die Randomisierung ausreichend Versuchspersonen pro Gruppe zur Verfügung stehen sollten. Hinsichtlich der konkreten Zahlen finden sich viele Unterschiede in der Literatur. Je nach Fragestellung kann man sich an dem Richtwert 30-40 Versuchspersonen pro Gruppe orientieren. | Bei der Randomisierung ist es sehr wichtig, dass das Gesetz der großen Zahlen berücksichtigt wird. Dieses besagt, dass für die Randomisierung ausreichend Versuchspersonen pro Gruppe zur Verfügung stehen sollten. Hinsichtlich der konkreten Zahlen finden sich viele Unterschiede in der Literatur. Je nach Fragestellung kann man sich an dem Richtwert 30-40 Versuchspersonen pro Gruppe orientieren. | ||
| Zeile 14: | Zeile 14: | ||
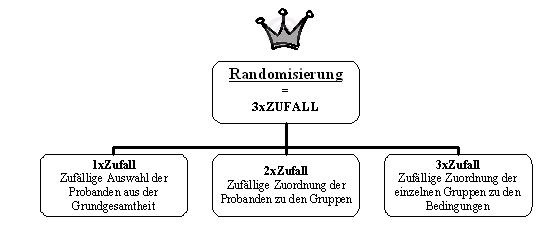
'''Übersicht Randomisierung''' | '''Übersicht Randomisierung''' | ||
[[Datei:Randomisierung.jpg|600px]] | [[Datei:Randomisierung.jpg|600px|link=Ausgelagerte_Bildbeschreibungen#Übersicht_Randomisierung|Ausgelagerte Bildbeschreibung von Übersicht Randomisierung]] | ||
'''Beispiel''' | '''Beispiel''' | ||
Aktuelle Version vom 13. Dezember 2021, 21:47 Uhr
Bei der Randomisierung wird angenommen, dass sich alle bekannten und unbekannten Merkmale der Versuchspersonen, die in einem Versuch als Störvariablen wirksam werden könnten, zufällig auf die Versuchbedingungen verteilen (Sarris, 1990). Sie ist eine der Kontrolltechniken zur Kontrolle der Sekundärvarianz in einem Experiment.
Die Randomisierung ist die sogenannte Königsdisziplin unter den Kontrolltechniken und wird mit der Faustregel 3x Zufall beschrieben: Zufällige Auswahl der Stichprobe aus der Grundgesamtheit (siehe Population), zufällige Einteilung der Versuchspersonen in die Versuchsgruppen und zufällige Zuteilung der Versuchsgruppen zu den einzelnen Versuchsbedingungen.
Es wird davon ausgegangen, dass sich alle unbekannten und bekannten Störvariablen per Zufall auf die verschiedenen Versuchsbedingungen verteilen. Dadurch sind die Gruppen und deren Ausgangswerte vergleichbar. Das Zufallsprinzip kann beispielsweise mit Würfeln oder Zufallszahlentabellen realisiert werden. Der große Vorteil des Randomisierungsprinzips ist die Kontrolle auch aller unbekannten Störvariablen. Die Versuchsgruppen unterscheiden sich also vor Versuchsbeginn nicht systematisch. Aus diesem Grund stellt die Randomisierung die ideale Kontrolltechnik zur Kontrolle der Sekundärvarianz dar. In der Praxis ist es häufig schwierig, tatsächlich das Prinzip im Sinne des "3xZufalls" zu realisieren. Stattdessen wird oft auf Quasiexperimentelle Pläne zurückgegriffen.
Bei der Randomisierung ist es sehr wichtig, dass das Gesetz der großen Zahlen berücksichtigt wird. Dieses besagt, dass für die Randomisierung ausreichend Versuchspersonen pro Gruppe zur Verfügung stehen sollten. Hinsichtlich der konkreten Zahlen finden sich viele Unterschiede in der Literatur. Je nach Fragestellung kann man sich an dem Richtwert 30-40 Versuchspersonen pro Gruppe orientieren. Stehen einem Versuchsleiter nicht genug Versuchspersonen zur Verfügung, ist es ratsam, ein anderes Versuchsdesign, etwa die Blockbildung oder die Wiederholungsmessung, zu wählen.
Übersicht Randomisierung
Beispiel
Eine Forschergruppe entscheidet sich auf Grund inhaltlicher Erwägungen, in ihrem nächsten Experiment das Randomisierungsprinzip zu realisieren. Hierfür rekrutiert sie 120 Versuchspersonen per Zufall aus einer Grundgesamtheit, wodurch die Forschergruppe eine repräsentative Stichprobe erhält ("1xZufall"). Diese 120 Probanden ordnen die Forscher per Zufallszahlentabellen in vier verschiedene Versuchsgruppen ein ("2xZufall"). Damit ist das Gesetz der großen Zahlen erfüllt [120/4 ≥ 30]. In einem dritten Schritt teilen sie die Versuchsgruppen per Würfelwurf den vier verschiedenen Bedingungen zu ("3xZufall").