Unvollständige Versuchspläne: Unterschied zwischen den Versionen
Diana (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
Elisa (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
||
| (4 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 22: | Zeile 22: | ||
*Lateinisches Quadrat | *Lateinisches Quadrat | ||
*Griechisch-Lateinisches Quadrat | *Griechisch-Lateinisches Quadrat | ||
{| class="wikitable" | |||
|- | |||
| - | |||
| A<sub>1</sub> | |||
| A<sub>2</sub> | |||
| A<sub>3</sub> | |||
| ... | |||
| A<sub>n</sub> | |||
|- | |||
| B<sub>1</sub> | |||
| C<sub>1</sub> | |||
| C<sub>2</sub> | |||
| C<sub>3</sub> | |||
| ... | |||
| C<sub>n</sub> | |||
|- | |||
| B<sub>2</sub> | |||
| C<sub>2</sub> | |||
| C<sub>3</sub> | |||
| C<sub>1</sub> | |||
| ... | |||
| C<sub>n</sub> | |||
|- | |||
| B<sub>3</sub> | |||
| C<sub>3</sub> | |||
| C<sub>1</sub> | |||
| C<sub>2</sub> | |||
| ... | |||
| C<sub>n</sub> | |||
|- | |||
| ... | |||
| ... | |||
| ... | |||
| ... | |||
| ... | |||
| C<sub>n</sub> | |||
|- | |||
| B<sub>n</sub> | |||
| C<sub>n</sub> | |||
| C<sub>n</sub> | |||
| C<sub>n</sub> | |||
| C<sub>n</sub> | |||
| C<sub>n</sub> | |||
|} | |||
Lateinisches Quadrat | |||
{| class="wikitable" | |||
|- | |||
| - | |||
| A<sub>1</sub> | |||
| A<sub>2</sub> | |||
| A<sub>3</sub> | |||
| ... | |||
| A<sub>n</sub> | |||
|- | |||
| B<sub>1</sub> | |||
| C<sub>1</sub>D<sub>1</sub> | |||
| C<sub>2</sub>D<sub>3</sub> | |||
| C<sub>3</sub>D<sub>2</sub> | |||
| ... | |||
| C<sub>n</sub>D<sub>n</sub> | |||
|- | |||
| B<sub>2</sub> | |||
| C<sub>2</sub>D<sub>2</sub> | |||
| C<sub>3</sub>D<sub>1</sub> | |||
| C<sub>1</sub>D<sub>3</sub> | |||
| ... | |||
| C<sub>n</sub>D<sub>n</sub> | |||
|- | |||
| B<sub>3</sub> | |||
| C<sub>3</sub>D<sub>3</sub> | |||
| C<sub>1</sub>D<sub>1</sub> | |||
| C<sub>2</sub>D<sub>2</sub> | |||
| ... | |||
| C<sub>n</sub>D<sub>n</sub> | |||
|- | |||
| ... | |||
| ... | |||
| ... | |||
| ... | |||
| ... | |||
| C<sub>n</sub>D<sub>n</sub> | |||
|- | |||
| B<sub>n</sub> | |||
| C<sub>n</sub>D<sub>n</sub> | |||
| C<sub>n</sub>D<sub>n</sub> | |||
| C<sub>n</sub>D<sub>n</sub> | |||
| C<sub>n</sub>D<sub>n</sub> | |||
| C<sub>n</sub>D<sub>n</sub> | |||
|} | |||
griechisch-lateinisches Quadrat | |||
''Beispiel: | ''Beispiel: | ||
In einem Experiment sollen unterschiedliche Einflussfaktoren auf die Konzentrationsleistung untersucht werden. Hierfür stehen 9 Versuchsgruppen mit jeweils 25 Probanden zur Verfügung. Untersucht werden soll der Einfluss von Schlafdauer, Kaffeekonsum und Frühsport. Ein Drittel der Probanden soll 8 Stunden schlafen, ein Drittel soll 4 Stunden schlafen und ein Drittel soll überhaupt nicht schlafen in der Nacht vor der Untersuchung. Ein Drittel bekommt am Morgen 3 Tassen Kaffee, ein Drittel bekommt eine Tasse Kaffee und ein Drittel bekommt keinen Kaffee. Zusätzlich soll ein Drittel der Probanden eine morgendliche Fitnessübung unter Anleitung machen, ein Drittel macht einen selbständigen Ausdauerlauf von 40 min und ein Drittel macht keinen Sport. ''<br/>Im Anschluss daran wird mit einem Test die Konzentrationsleistung erhoben. Da lediglich 9 (statt der nötigen 27) Versuchsgruppen zur Verfügung stehen kommt hier nur ein unvollständiges Design infrage. So können Haupteffekte zu den einzelnen Faktoren, aber keine Interaktionseffekte überprüft werden. Die folgenden Faktorstufenkombinationen werden in einem lateinischen Quadratplan untersucht:'' | In einem Experiment sollen unterschiedliche Einflussfaktoren auf die Konzentrationsleistung untersucht werden. Hierfür stehen 9 Versuchsgruppen mit jeweils 25 Probanden zur Verfügung. Untersucht werden soll der Einfluss von Schlafdauer, Kaffeekonsum und Frühsport. Ein Drittel der Probanden soll 8 Stunden schlafen, ein Drittel soll 4 Stunden schlafen und ein Drittel soll überhaupt nicht schlafen in der Nacht vor der Untersuchung. Ein Drittel bekommt am Morgen 3 Tassen Kaffee, ein Drittel bekommt eine Tasse Kaffee und ein Drittel bekommt keinen Kaffee. Zusätzlich soll ein Drittel der Probanden eine morgendliche Fitnessübung unter Anleitung machen, ein Drittel macht einen selbständigen Ausdauerlauf von 40 min und ein Drittel macht keinen Sport. ''<br/>Im Anschluss daran wird mit einem Test die Konzentrationsleistung erhoben. Da lediglich 9 (statt der nötigen 27) Versuchsgruppen zur Verfügung stehen kommt hier nur ein unvollständiges Design infrage. So können Haupteffekte zu den einzelnen Faktoren, aber keine Interaktionseffekte überprüft werden. Die folgenden Faktorstufenkombinationen werden in einem lateinischen Quadratplan untersucht:'' | ||
{| class="wikitable" | |||
|- | |||
| - | |||
| style="background-color:#79a2b0;" | A<sub>1</sub><br />0 Stunden | |||
| style="background-color:#79a2b0;" | A<sub>2</sub><br />4 Stunden | |||
| style="background-color:#79a2b0;" | A<sub>3</sub><br />8 Stunden | |||
|- style="background-color:#bfa5e3;" | |||
| style="background-color:#c9e9f0;" | B<sub>1</sub><br />0 Tassen | |||
| style="color:#000000;" | C<sub>1</sub><br />kein Sport | |||
| style="color:#000000;" | C<sub>2</sub><br />Ausdauerlauf | |||
| style="color:#000000;" | C<sub>3</sub><br />Fitnessübung | |||
|- style="background-color:#bfa5e3;" | |||
| style="background-color:#c9e9f0;" | B2<br />1 Tasse | |||
| style="color:#000000;" | C<sub>2</sub><br />Ausdauerlauf | |||
| style="color:#000000;" | C<sub>3</sub><br />Fitnessübung | |||
| style="color:#000000;" | C<sub>1</sub><br />kein Sport | |||
|- style="background-color:#bfa5e3;" | |||
| style="background-color:#c9e9f0;" | B2<br />3 Tassen | |||
| style="color:#000000;" | C<sub>3</sub><br />Fitnessübung | |||
| style="color:#000000;" | C<sub>1</sub><br />kein Sport | |||
| style="color:#000000;" | C<sub>2</sub><br />Ausdauerlauf | |||
|} | |||
== Hierarchische Versuchspläne == | == Hierarchische Versuchspläne == | ||
| Zeile 37: | Zeile 150: | ||
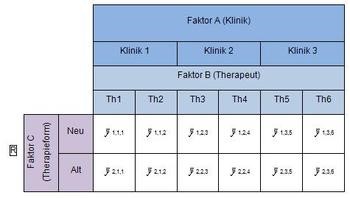
''<br/>Ein Forscher möchte eine neue Therapieform evaluieren. Hierfür stehen ihm insgesamt 120 Patienten von 3 Kliniken zur Verfügung. Er weiß, dass verschiedene Therapeuten und ein unterschiedliches Ambiente vermutlich auch den Therapieerfolg mit beeinflussen können. Daher bezieht er diese Faktoren in sein Untersuchungsdesign mit ein. | ''<br/>Ein Forscher möchte eine neue Therapieform evaluieren. Hierfür stehen ihm insgesamt 120 Patienten von 3 Kliniken zur Verfügung. Er weiß, dass verschiedene Therapeuten und ein unterschiedliches Ambiente vermutlich auch den Therapieerfolg mit beeinflussen können. Daher bezieht er diese Faktoren in sein Untersuchungsdesign mit ein. | ||
''<br/>Es wäre unsinnig, die verschiedenen Therapeuten mit den verschiedenen Kliniken zu kombinieren. Daher werden die Faktoren A und B ineinander verschachtelt. So kann der Forscher im Ergebnis erkennen, ob der Haupteffekt C in unterschiedlichem Ambiente und bei unterschiedlichen Therapeuten anders ausfällt.'' | ''<br/>Es wäre unsinnig, die verschiedenen Therapeuten mit den verschiedenen Kliniken zu kombinieren. Daher werden die Faktoren A und B ineinander verschachtelt. So kann der Forscher im Ergebnis erkennen, ob der Haupteffekt C in unterschiedlichem Ambiente und bei unterschiedlichen Therapeuten anders ausfällt.'' | ||
<br/> [[Datei:UnvVP3.jpg]] | <br/> [[Datei:UnvVP3.jpg|link=Ausgelagerte_Bildbeschreibungen#Versuchsplan_Klinik|Ausgelagerte Bildbeschreibung von Versuchsplan Klinik]] | ||
Aktuelle Version vom 9. Dezember 2021, 14:32 Uhr
Unvollständige Versuchspläne sind mehrfaktorielle Designs, in denen nicht alle Stufen jedes Faktors miteinander kombiniert werden.
In einem vollständigen mehrfaktoriellen Design werden die Stufen jeder unabhängigen Variable untereinander kombiniert. So entstehen in einem 2x2-faktoriellen Design beispielsweise 4 Faktorstufenkombinationen. In unvollständigen Versuchsplänen werden nicht alle Stufen miteinander kombiniert.
Das kann zwei Gründe haben. Entweder sind nicht alle Kombinationen möglich (z.B. kann man Patienten nicht zwangsverlegen in eine andere Klinik nur für eine Studie) oder aber manche Kombinationen sind inhaltlich nicht sinnvoll.
Unvollständige Versuchspläne sind im Vergleich zu mehrfaktoriellen Plänen ökonomischer, da weniger Versuchspersonen benötigt werden. Sie haben aber auch einen entscheidenden Nachteil. Während bei mehrfaktoriellen Designs immer alle Haupteffekte und Interaktionseffekte überprüft werden können, gilt dies für unvollständige Pläne nicht. Vor allem Interaktionseffekte sind in der Regel nicht interpretierbar. Diese Interpretationseinschränkungen sind immer zu berücksichtigen bei der Entscheidung für ein unvollständiges Versuchsdesign. Man sollte sich nur dann für einen solchen Plan entscheiden, wenn Interaktionseffekte ausgeschlossen oder als irrelevant eingestuft werden können. Es gibt zwei Arten von unvollständigen Versuchsplänen, die sich hinsichtlich ihrer Struktur unterscheiden:
- Hierarchische Pläne
- Quadratische Pläne
Quadratische Versuchspläne
Quadratische Pläne sind unvollständige, mehrfaktorielle Versuchspläne mit drei oder vier Faktoren. Da ihre Faktoren je die gleiche Stufenanzahl haben, ergibt sich ein Quadrat. Sie basieren auf einem vollständigen zweifaktoriellen Design, in welches nach dem Prinzip der zyklischen Permutation weitere Faktoren eingefügt werden.
In quadratischen Plänen werden nicht alle Faktorstufen untereinander kombiniert, sondern nur teilweise. Es treten z.B. im lateinischen Quadrat nur alle 2er-Kombinationen, nicht jedoch alle 3er-Kombinationen auf.
Quadratische Versuchspläne sind wie alle unvollständigen Versuchspläne im Vergleich zu mehrfaktoriellen Plänen ökonomischer, da weniger Versuchspersonen benötigt werden. Sie haben aber auch einen entscheidenden Nachteil. Während bei mehrfaktoriellen Designs immer alle Haupteffekte und Interaktionseffekte überprüft werden können, gilt dies für unvollständige Pläne nicht. Mit quadratischen Plänen sind keine Interaktionseffekte prüfbar. Haupteffekte lassen sich hingegen prüfen. Man sollte sich nur dann für ein solches Design entscheiden, wenn Interaktionseffekte ausgeschlossen oder als irrelevant eingestuft werden können.
Arten:
- Lateinisches Quadrat
- Griechisch-Lateinisches Quadrat
| - | A1 | A2 | A3 | ... | An |
| B1 | C1 | C2 | C3 | ... | Cn |
| B2 | C2 | C3 | C1 | ... | Cn |
| B3 | C3 | C1 | C2 | ... | Cn |
| ... | ... | ... | ... | ... | Cn |
| Bn | Cn | Cn | Cn | Cn | Cn |
Lateinisches Quadrat
| - | A1 | A2 | A3 | ... | An |
| B1 | C1D1 | C2D3 | C3D2 | ... | CnDn |
| B2 | C2D2 | C3D1 | C1D3 | ... | CnDn |
| B3 | C3D3 | C1D1 | C2D2 | ... | CnDn |
| ... | ... | ... | ... | ... | CnDn |
| Bn | CnDn | CnDn | CnDn | CnDn | CnDn |
griechisch-lateinisches Quadrat
Beispiel:
In einem Experiment sollen unterschiedliche Einflussfaktoren auf die Konzentrationsleistung untersucht werden. Hierfür stehen 9 Versuchsgruppen mit jeweils 25 Probanden zur Verfügung. Untersucht werden soll der Einfluss von Schlafdauer, Kaffeekonsum und Frühsport. Ein Drittel der Probanden soll 8 Stunden schlafen, ein Drittel soll 4 Stunden schlafen und ein Drittel soll überhaupt nicht schlafen in der Nacht vor der Untersuchung. Ein Drittel bekommt am Morgen 3 Tassen Kaffee, ein Drittel bekommt eine Tasse Kaffee und ein Drittel bekommt keinen Kaffee. Zusätzlich soll ein Drittel der Probanden eine morgendliche Fitnessübung unter Anleitung machen, ein Drittel macht einen selbständigen Ausdauerlauf von 40 min und ein Drittel macht keinen Sport.
Im Anschluss daran wird mit einem Test die Konzentrationsleistung erhoben. Da lediglich 9 (statt der nötigen 27) Versuchsgruppen zur Verfügung stehen kommt hier nur ein unvollständiges Design infrage. So können Haupteffekte zu den einzelnen Faktoren, aber keine Interaktionseffekte überprüft werden. Die folgenden Faktorstufenkombinationen werden in einem lateinischen Quadratplan untersucht:
| - | A1 0 Stunden |
A2 4 Stunden |
A3 8 Stunden |
| B1 0 Tassen |
C1 kein Sport |
C2 Ausdauerlauf |
C3 Fitnessübung |
| B2 1 Tasse |
C2 Ausdauerlauf |
C3 Fitnessübung |
C1 kein Sport |
| B2 3 Tassen |
C3 Fitnessübung |
C1 kein Sport |
C2 Ausdauerlauf |
Hierarchische Versuchspläne
Hierarchische Pläne sind unvollständige, mehrfaktorielle Versuchspläne und zeichnen sich durch eine hierarchische Verschachtelung der Faktoren aus. In hierarchischen Plänen werden nicht alle Faktorstufen untereinander kombiniert, sondern nur teilweise. Beispielsweise wird der Stufe A1 eine Teilmenge des Faktors B zugeordnet und der Stufe A2 die andere Teilmenge. Hierarchische Versuchspläne sind wie alle unvollständigen Versuchspläne im Vergleich zu mehrfaktoriellen Plänen ökonomischer, da weniger Versuchspersonen benötigt werden. Sie haben aber auch einen entscheidenden Nachteil. Während bei mehrfaktoriellen Designs immer alle Haupteffekte und Interaktionseffekte überprüft werden können, gilt dies für unvollständige Pläne nicht. Mit hierarchischen Plänen sind keine, mit teilhierarchischen Plänen nur einige Interaktionseffekte prüfbar. Haupteffekte lassen sich prüfen. Man sollte sich nur dann für ein solches Design entscheiden, wenn Interaktionseffekte ausgeschlossen oder als irrelevant eingestuft werden können.
Beispiel eines vollständigen hierarchischen Plans:
Ein Forscher möchte eine neue Therapieform evaluieren. Hierfür stehen ihm insgesamt 120 Patienten von 3 Kliniken zur Verfügung. Er weiß, dass verschiedene Therapeuten und ein unterschiedliches Ambiente vermutlich auch den Therapieerfolg mit beeinflussen können. Daher bezieht er diese Faktoren in sein Untersuchungsdesign mit ein.
Es wäre unsinnig, die verschiedenen Therapeuten mit den verschiedenen Kliniken zu kombinieren. Daher werden die Faktoren A und B ineinander verschachtelt. So kann der Forscher im Ergebnis erkennen, ob der Haupteffekt C in unterschiedlichem Ambiente und bei unterschiedlichen Therapeuten anders ausfällt.