Statistische Modelle: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Paul (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
||
| (5 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 29: | Zeile 29: | ||
: [[Datei:Statistische_Modelle_2.png|link=Ausgelagerte_Formeln#Hyperbolisches Discounting|Ausgelagerte Formel Hyperbolisches Discounting]] | : [[Datei:Statistische_Modelle_2.png|link=Ausgelagerte_Formeln#Hyperbolisches Discounting|Ausgelagerte Formel Hyperbolisches Discounting]] | ||
: Den sogenannten Diskontierungsfaktor stellt dabei der Parameter k dar. Der subjektive Wert der Belohnung nimmt nach dieser Funktion mit zunehmend kleineren Prozentanteilen ab, je größer die Zeitspanne bis zum Erhalt der Belohnung ist. Verschiedene Studien konnten zeigen, dass dieses Modell besser in der Lage ist, empirische Daten zu modellieren. Die Verwendung des exponentiellen Modells überschätzt den subjektiven Wert einer Belohnung nach kurzen Zeitintervallen und unterschätzt deren Wert nach längeren Intervallen. Eine Weiterentwicklung des hyperbolischen Modells stellt das '''''Hyperboloid Modell''''' dar. Dabei wird der Nenner des Bruchs der Gleichung potenziert: | : Den sogenannten Diskontierungsfaktor stellt dabei der Parameter k dar. Der subjektive Wert der Belohnung nimmt nach dieser Funktion mit zunehmend kleineren Prozentanteilen ab, je größer die Zeitspanne bis zum Erhalt der Belohnung ist. Verschiedene Studien konnten zeigen, dass dieses Modell besser in der Lage ist, empirische Daten zu modellieren. Die Verwendung des exponentiellen Modells überschätzt den subjektiven Wert einer Belohnung nach kurzen Zeitintervallen und unterschätzt deren Wert nach längeren Intervallen. Eine Weiterentwicklung des hyperbolischen Modells stellt das '''''Hyperboloid Modell''''' dar. Dabei wird der Nenner des Bruchs der Gleichung potenziert: | ||
: [[Datei:Statistische_Modelle_3.png]] | : [[Datei:Statistische_Modelle_3.png|link=Ausgelagerte_Formeln#Hyperboloid Modell|Ausgelagerte Formel Hyperboloid Modell]] | ||
: Dieses allgemeinere Modell ist oftmals in der Lage, die vorliegenden Daten noch besser abzubilden – zu fitten. | : Dieses allgemeinere Modell ist oftmals in der Lage, die vorliegenden Daten noch besser abzubilden – zu fitten. | ||
| Zeile 39: | Zeile 39: | ||
: Das Modell des quasi-hyperbolischen Discountings ermittelt den subjektiven Wert einer verzögerten Belohnung mithilfe des Wertes, den die Belohnung hätte, wenn sie sofort verfügbar wäre, vermindert um zwei Faktoren: die exponentielle Abwertung δ, welche die Verminderung des Wertes um einen fixen Anteil für jeden Zeitschritt, den die Belohnung weiter in die Zukunft verschoben wird, darstellt und einen Parameter β, welcher eine überproportionale Gewichtung sofortiger Belohnung integriert. Dabei erfolgt eine Verminderung des subjektiven Wertes aller zukünftigen Belohnungen um den gleichen konstanten Prozentsatz β. Der subjektive Wert einer Belohnung berechnet sich somit mittels folgender Formeln: | : Das Modell des quasi-hyperbolischen Discountings ermittelt den subjektiven Wert einer verzögerten Belohnung mithilfe des Wertes, den die Belohnung hätte, wenn sie sofort verfügbar wäre, vermindert um zwei Faktoren: die exponentielle Abwertung δ, welche die Verminderung des Wertes um einen fixen Anteil für jeden Zeitschritt, den die Belohnung weiter in die Zukunft verschoben wird, darstellt und einen Parameter β, welcher eine überproportionale Gewichtung sofortiger Belohnung integriert. Dabei erfolgt eine Verminderung des subjektiven Wertes aller zukünftigen Belohnungen um den gleichen konstanten Prozentsatz β. Der subjektive Wert einer Belohnung berechnet sich somit mittels folgender Formeln: | ||
: für t = 0: [[Datei:Statistische_Modelle_4.png]] | : für t = 0: [[Datei:Statistische_Modelle_4.png|link=Ausgelagerte_Formeln#Quasi-hyperbolisches Discounting t = 0|Ausgelagerte Formel für subjektiver Wert einer Belohnung für t = 0]] | ||
: für t > 0: [[Datei:Statistische_Modelle_5.png]] | : für t > 0: [[Datei:Statistische_Modelle_5.png|link=Ausgelagerte_Formeln#Quasi-hyperbolisches Discounting t > 0|Ausgelagerte Formel für subjektiver Wert einer Belohnung für t > 0]] | ||
: Gilt β = 1 entspricht dieses Modell somit dem exponentiellen Discounting. | : Gilt β = 1 entspricht dieses Modell somit dem exponentiellen Discounting. | ||
| Zeile 49: | Zeile 49: | ||
Parameterwerte: U(x) = 5; k= δ = 0.8; β = 0.7 | Parameterwerte: U(x) = 5; k= δ = 0.8; β = 0.7 | ||
[[Datei:Statistische_Modelle_6.png|700px]] <br /> | [[Datei:Statistische_Modelle_6.png|700px|link=Ausgelagerte_Bildbeschreibungen#Beispiel Statistische Modelle|Ausgelagerte Bildbeschreibung von Beispiel Statistische Modelle]] <br /> | ||
Aktuelle Version vom 13. Februar 2022, 22:17 Uhr
Statistische Modelle zählen zu den Grundlagen des Denkmodells der empirischen Psychologie und verfolgen das Ziel, Parameter aus existierenden Daten zu schätzen, um die Daten möglichst gut zusammenzufassen bzw. zu beschreiben, latente, also in den Daten versteckte Merkmale zu extrahieren und gegebenenfalls Parameterwerte für neue Individuen vorherzusagen.
Beispiele für statistische Modelle stellen unter anderem Verteilungsmodelle, Sequential Sampling Modelle, psychometrische Funktionen und das Allgemeine Lineare Modell (GLM) dar.
Eine vereinfachte Beschreibbarkeit der Daten erreichen diese Modelle oftmals durch Abstraktion und Reduzierung unwesentlicher Informationen – sie versuchen sozusagen aus dem unvermeidlichen Rauschen einer empirischen Messung das Signal herauszufiltern. Ein Beispiel wäre bereits die Berechnung von Mittelwerten und Standardabweichungen, welche auf der Annahme beruht, dass die Daten einer Normalverteilung folgen und sich anhand der Parameter dieses Datenmodells (der Normalverteilungskurve) die Daten exakt beschreiben lassen. Diese Vereinfachung führt jedoch zu Abweichungen gegenüber den Originaldaten, welche man als „Fehler“ bezeichnet. Diesen Fehler versucht man durch das Fitten des Modells an die Daten zu minimieren. Ein Vergleich der empirischen mit den modellierten Daten erlaubt anschließend die Beurteilung der Beschreibungsgüte (Güte des Fits) des Modells.
Aufgrund der Tatsache, dass statistische Modelle überhaupt erst aus existierenden Daten gewonnen werden können und dann zur Beschreibung dieser Fälle verwendet werden, sind sie in der Regel nicht uneingeschränkt auf andere Fälle übertragbar. Da sie lediglich versuchen, Daten auf einer abstrakten Ebene zu beschreiben bzw. zusammenzufassen, können Sie zumeist auch keine überraschenden Vorhersagen machen. Da diese Modelle nur Beschreibungen und keine mechanistischen Erklärungen darstellen, können Sie sich zudem nicht verhalten und somit nicht zur Simulation neuer Untersuchungen dienen.
Deutlich werden diese Sachverhalte, wenn wir einen Vergleich mit dem Modell der Gravitation von Newton ziehen: Wenn wir immer wieder Aufenthaltsorte von Planeten am Himmel messen, so mögen wir in der Lage sein, die entstehenden Punkte auf einer Karte durch elliptische Bahnen abstrakt zusammenzufassen. So mag es dann auch möglich sein, auf Basis der abstrakten elliptischen Bahnen einen zukünftigen Aufenthaltsort für einen Planeten vorherzusagen. Weiter werden wir mit diesen einfachen Beschreibungen der Daten aber nicht kommen, denn wir haben die Daten nur beschrieben, aber können nicht erklären, wie sie entstehen, welche physikalischen Gesetze dahinterstehen. Erst Newtons Beschreibung der mechanistischen Zusammenhänge zwischen Himmelkörpern erlaubt es, über die gemessenen Daten hinauszugehen und anhand der gemessenen Bahnen neue Planeten vorherzusagen (und dann empirisch zu finden) – also auf Basis der Daten und der angenommenen Zusammenhänge auch neue Vorhersagen zu machen. Diese Formeln Newtons stellen ein mathematisches Modell der Bewegung von Himmelskörpern dar, im Gegensatz zu den Kreisbahnen, die lediglich die gemessenen Punkte sparsam zusammenfassen.
Funktionen zur Beschreibung von Verhalten am Beispiel von Discounting Modellen
„Warum schaffe ich es nur so selten, meine guten Vorsätze für das neue Semester umzusetzen?“ Diese Frage haben sich die meisten von uns wahrscheinlich bereits wiederholt stellen müssen. Viele scheitern daran, ihre ehrgeizigen Vorhaben, wie rechtzeitig mit dem Lernen zu beginnen, in Gegenwart alternativer Freizeitgestaltungsmöglichkeiten aufrechtzuerhalten. Und das, obwohl ihnen die gute Abschlussnote durchaus wichtiger sein kann als der freie Nachmittag im Schwimmbad. Die Ursache scheint klar: Der Tag in der Sonne verspricht eine sofortige Belohnung, bis zur Ausgabe des Zeugnisses vergeht noch viel Zeit. Würden Menschen streng nach einem Nutzenmaximierungsprinzip handeln, sollten sie sich jedoch trotzdem für einen Tag in der Bücherei entscheiden, wenn dieser eine größere Belohnung verspricht. In der Realität tun sie das eher selten. Es ist somit notwendig, ein alternatives Erklärungsmodell zu finden, welches in der Lage ist, die Präferenzen von Menschen über längere Zeiträume hinweg zu modellieren. Diese Aufgabe erfüllen sogenannte Discounting Modelle (= Diskontierungsmodelle). Die Grundidee dieser Modelle ist, dass Menschen den Wert entfernter Belohnungen für sich persönlich diskontieren (= abwerten) und somit sofortige Belohnungen solchen, die erst in der Zukunft eintreten, vorziehen. Man bezeichnet dieses Phänomen als Delay Discounting (oder auch Temporal Discounting, Time Reference, Time Discounting).
Discounting Modelle sind statistische Modelle, die das Wahlverhalten einer Person anhand einer einfachen mathematischen Funktion beschreiben: Der empfundene Wert einer Belohnung (= der subjektive Wert) wird als eine Funktion der Zeitspanne, bis man die Belohnung erhält (und weiterer Einflussgrößen) beschrieben. Anhand der Funktion ist es möglich, menschliche Entscheidungen zu beschreiben und aus existierendem Wahlverhalten eine Vorhersage zukünftigen Entscheidungsverhaltens zu treffen. Oftmals wird das Modell, wie auch in diesem Artikel, anhand finanzieller Entscheidungen erklärt. Es lässt sich jedoch auch auf andere Anwendungskontexte (z.B. subjektive Werte zukünftiger Belohnungen in Form von Konsumgütern, verfügbaren Urlaubstagen, …) übertragen. Ebenso können Funktionen nicht nur zur Beschreibung von Discounting, sondern auch vielen anderen Arten von Verhalten verwendet werden (z.B. Vergessenskurven, welche die noch vorhandenen Gedächtnisinhalte anhand der vergangenen Zeit beschreiben).
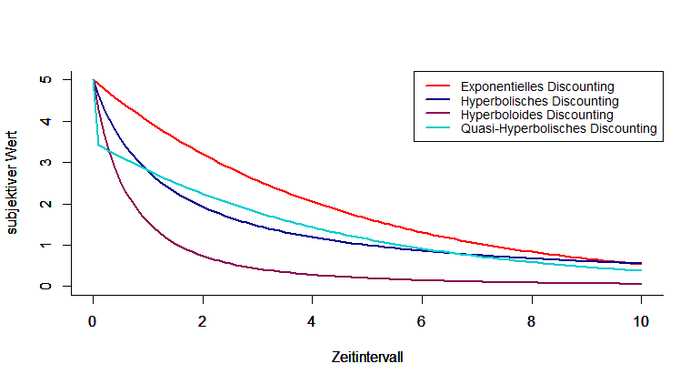
Das Modell des Discountings besteht aus drei entscheidenden Komponenten: dem subjektiv wahrgenommenen Wert der Belohnung, dem subjektiv wahrgenommenen Wert der Zeit und der Kombination dieser beiden Elemente. Wie genau die Elemente kombiniert werden und wie viele Parameter im Modell enthalten sind, darin unterscheiden sich verschiedene Modelle/ Funktionen. Man unterscheidet exponentielles Discounting, hyperbolisches Discounting, quasi-hyperbolisches Discounting, hyperboloides Discounting, arithmetisches Discounting und viele mehr. Einige dieser Formen sollen im Folgenden näher betrachtet und in der Abbildung gegenübergestellt werden. Eine detaillierte Beschreibung der Verfahren findet sich im Übersichtsartikel von Doyle (2013).
- Exponentielles Discounting
- Beim exponentiellen Discounting ergibt sich der subjektive Wert einer Belohnung durch die folgende Gleichung:
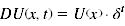
- DU(x,t) steht dabei für den subjektiven Wert der Belohnung x nach einer Zeitspanne t, U(x) ist der absolute Betrag der Belohnung und δ entspricht einem Parameter, welcher das Ausmaß der Abwertung beschreibt. Für t wird in die Formel die Zeitspanne bis zum Erhalt der Belohnung eingesetzt. Nach dieser Funktion nimmt der subjektive Wert mit jeder schrittweisen Vergrößerung der Zeitspanne, bis zum Erhalt der Belohnung, um einen festen Prozentanteil ab.
- Hyperbolisches Discounting
- Der subjektive Wert einer Belohnung beim hyperbolischen Discounting berechnet sich folgendermaßen:
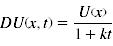
- Den sogenannten Diskontierungsfaktor stellt dabei der Parameter k dar. Der subjektive Wert der Belohnung nimmt nach dieser Funktion mit zunehmend kleineren Prozentanteilen ab, je größer die Zeitspanne bis zum Erhalt der Belohnung ist. Verschiedene Studien konnten zeigen, dass dieses Modell besser in der Lage ist, empirische Daten zu modellieren. Die Verwendung des exponentiellen Modells überschätzt den subjektiven Wert einer Belohnung nach kurzen Zeitintervallen und unterschätzt deren Wert nach längeren Intervallen. Eine Weiterentwicklung des hyperbolischen Modells stellt das Hyperboloid Modell dar. Dabei wird der Nenner des Bruchs der Gleichung potenziert:
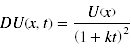
- Dieses allgemeinere Modell ist oftmals in der Lage, die vorliegenden Daten noch besser abzubilden – zu fitten.
- Das exponentielle und das hyperbolische Modell unterscheiden sich nicht nur in ihrer Überstimmung mit empirischen Daten. Sie treffen auch unterschiedliche Annahmen bezüglich der sogenannten Präferenzumkehrung. Das hyperbolische Modell sagt dabei einen Wechsel der Präferenzen in Abhängigkeit der Zeitspanne bis zum Erhalt der Belohnung vorher. Das exponentielle Modell tut dies nicht. Folgendes Beispiel soll diesen Sachverhalt verdeutlichen:
- Der subjektive Wert eines niedrigeren (500 €) und eines hohen Geldbetrages (1000 €) ist relativ gering, wenn die Zeitspanne, bis man diesen Betrag erhält, sehr groß ist. Er beträgt zum Beispiel rund 200 €, wenn man auf den niedrigeren Betrag ein Jahr und auf den höheren Betrag zwei Jahre warten muss. Verkürzt sich die Zeitspanne jedoch, kehrt sich das Verhältnis um. Nach fast einem Jahr, steigt der subjektive Wert des geringeren Betrags auf fast 500 € an, während der subjektive Wert der 1000 €, auf welche man ein weiteres Jahr warten muss, niedrig bleibt. Der subjektive Wert der 1000 € ist somit ab einem bestimmten Zeitpunkt geringer als der subjektive Wert der 500 €, deren Erhalt nun in naher Zukunft liegt. Eine solche Präferenzumkehrung kann beim exponentiellen Discounting nicht auftreten.
- Quasi-Hyperbolisches Discounting
- Das Modell des quasi-hyperbolischen Discountings ermittelt den subjektiven Wert einer verzögerten Belohnung mithilfe des Wertes, den die Belohnung hätte, wenn sie sofort verfügbar wäre, vermindert um zwei Faktoren: die exponentielle Abwertung δ, welche die Verminderung des Wertes um einen fixen Anteil für jeden Zeitschritt, den die Belohnung weiter in die Zukunft verschoben wird, darstellt und einen Parameter β, welcher eine überproportionale Gewichtung sofortiger Belohnung integriert. Dabei erfolgt eine Verminderung des subjektiven Wertes aller zukünftigen Belohnungen um den gleichen konstanten Prozentsatz β. Der subjektive Wert einer Belohnung berechnet sich somit mittels folgender Formeln:
- für t = 0:
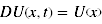
- für t > 0:
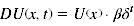
- Gilt β = 1 entspricht dieses Modell somit dem exponentiellen Discounting.
Die Abbildung stellt die Veränderung des subjektiven Wertes einer Belohnung in Abhängigkeit der Zeitspanne, bis zum Erhalt dieser Belohnung, für verschiedene Discounting-Modelle dar.
Parameterwerte: U(x) = 5; k= δ = 0.8; β = 0.7