Level: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
{{Nav|Navigation|Kognitive Modellierung|Hauptseite}} | {{Nav|Navigation|Kognitive Modellierung|Hauptseite}} | ||
Bevor man einen Datensatz [[Fitting & Parameter Estimation|fitten]] kann, muss die Entscheidung getroffen werden, auf welcher Ebene die Daten modelliert werden sollen. Hier gibt es drei Ansätze: Beim [[Fitting & Parameter Estimation|Fitten]] auf der Aggregatebene fasst man die Daten aller Versuchspersonen zusammen, während beim [[Fitting & Parameter Estimation|Fitten]] auf der Individualebene jede Versuchsperson eigene Parameterwerte zugewiesen bekommt. Einen Kompromiss stellt das hierarchische [[Fitting & Parameter Estimation|Fitten]] dar, bei dem einige Parameter für alle Versuchspersonen zusammen (also auf Aggregatebene), weitere aber pro Bedingungen oder auch individuell geschätzt werden können. Alle genannten Ansätze werden im Folgenden genauer beschrieben. | Bevor man einen Datensatz [[Fitting & Parameter Estimation|fitten]] kann, muss die Entscheidung getroffen werden, auf welcher Ebene die Daten modelliert werden sollen. Hier gibt es drei Ansätze: Beim [[Fitting & Parameter Estimation|Fitten]] auf der Aggregatebene fasst man die Daten aller Versuchspersonen zusammen, während beim [[Fitting & Parameter Estimation|Fitten]] auf der Individualebene jede Versuchsperson eigene Parameterwerte zugewiesen bekommt. Einen Kompromiss stellt das hierarchische [[Fitting & Parameter Estimation|Fitten]] dar, bei dem einige Parameter für alle Versuchspersonen zusammen (also auf Aggregatebene), weitere aber pro Bedingungen oder auch individuell geschätzt werden können. Alle genannten Ansätze werden im Folgenden genauer beschrieben. | ||
Version vom 24. August 2018, 20:25 Uhr
Bevor man einen Datensatz fitten kann, muss die Entscheidung getroffen werden, auf welcher Ebene die Daten modelliert werden sollen. Hier gibt es drei Ansätze: Beim Fitten auf der Aggregatebene fasst man die Daten aller Versuchspersonen zusammen, während beim Fitten auf der Individualebene jede Versuchsperson eigene Parameterwerte zugewiesen bekommt. Einen Kompromiss stellt das hierarchische Fitten dar, bei dem einige Parameter für alle Versuchspersonen zusammen (also auf Aggregatebene), weitere aber pro Bedingungen oder auch individuell geschätzt werden können. Alle genannten Ansätze werden im Folgenden genauer beschrieben.
Aggretagebene
Beim Fitten auf der Aggregatebene wird ein Parameterset für jede Bedingung des Experiments bestimmt. Dabei werden die Daten aller Versuchspersonen einbezogen, sodass das Modell letztlich einen Durchschnittsprobanden beschreiben soll. Der Ansatz eignet sich, um einen allgemeinen Prozess zu beschreiben, vernachlässigt jedoch interindividuelle Differenzen. Wenn man über wenige Daten jedes einzelnen Probanden verfügt, kann das Fitten auf Aggregatebene der einzige Weg sein, um überhaupt einen quantitativen Fit zu erreichen.
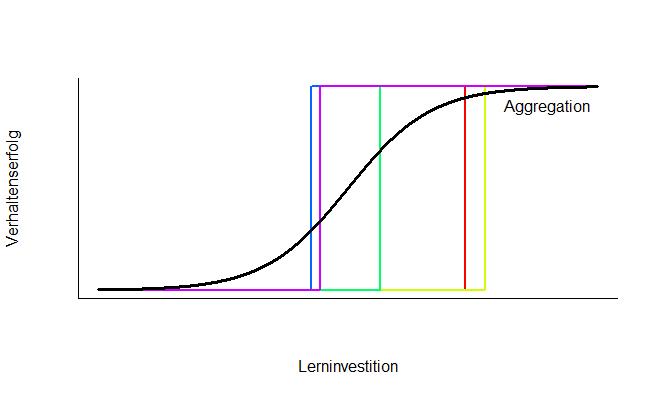
Zu beachten ist, dass dieses Vorgehen, wie alle Auswertungen auf Aggregatsebene, ein falsches Modell als wahr erscheinen lassen kann, wie im nachfolgenden Beispiel verdeutlicht wird. Bei Lernaufgaben ist es oft so, dass der Erfolg bei der Aufgabenbearbeitung der Versuchsperson eine Weile auf Zufallsniveau liegt, bis es einen plötzlichen Sprung zur korrekten Lösung gibt. Ein stufenförmiger Graph beschreibt den Prozess bestmöglich (siehe farbige Stufen in der Grafik). Da der Sprung bei jedem Probanden aber zu einem anderen Zeitpunkt erfolgt, würde die Aggregation der Daten eines solchen Prozesses dafür sorgen, dass ein gradueller, sanfter Anstieg des Bearbeitungserfolgs angenommen wird. Diese Glättung entspricht aber nicht mehr dem, wie der Prozess auf individualebene tatsächlich funktioniert. Beim Fitten auf Aggregatebene sollte also immer überprüft werden, inwiefern das Ergebnis die Daten der einzelnen Individuen widerspiegelt.
Individualebene
Beim Fitten auf der Individualebene wird ein Parameterset für jede Bedingung und für jeden Probanden einzeln bestimmt. So wird eine unangebrachte Glättung vermieden. Der Ansatz ist zwingend notwendig, wenn nicht allgemeine Prozesse, sondern individuelle Unterschiede untersucht werden sollen. Zudem können die individuellen Parameter genutzt werden, um eine Gruppenverteilung der Parameter zu erstellen, sodass statistische Tests durchgeführt werden können. Beispielsweise könnte für zwei Personengruppen mit einem t-Test herausgefunden werden, ob sich ein bestimmter Parameter zwischen den Gruppen signifikant unterscheidet. Von Nachteil ist bei der individuellen Modellierung jedoch, dass sie sehr viele Datenpunkte benötigt, da individuelle Daten mehr Rauschen enthalten als aggregierte. Außerdem sind Gütekriterien wie die Reliabilität der Parameterschätzung zu überprüfen.
Hierarchische Modellierung
Bei der hierarchischen Vorgehensweise können Parameter auf verschiedenen Ebenen geschätzt werden. Einzelne Parameter werden für alle Versuchspersonen kombiniert geschätzt, während ausgewählte Parameter personen- oder bedingungsspezifisch bestimmt werden. Der Ansatz kombiniert also die Vorteile der beiden anderen Ansätze und hilft, Probleme der Aggregatebene und der Individualebene zu umgehen. Er führt jedoch zu einem hohen Komplexitätsgrad, was bei der Optimierung zu Schwierigkeiten führen kann.