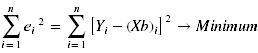General Linear Model: Unterschied zwischen den Versionen
Wehner (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
Wehner (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
||
| Zeile 8: | Zeile 8: | ||
: [[Datei:GLM_1.png]] | : [[Datei:GLM_1.png]] | ||
Y... Vektor der Kriteriumsvariablen | |||
X... Matrix der Prädiktoren (= Designmatrix) | |||
b... Vektor der Gewichte aller Prädiktoren | |||
e... Vektor der Residuen | |||
Die gleichzeitige Betrachtung der Werte mehrerer Beobachtungseinheiten (z.B. Individuen) führt zu einem linearen Gleichungssystem, welches mit Hilfe eines Minimierungsprinzips (dem Prinzip der Kleinsten Quadrate) die Schätzung der gesuchten Prädiktorgewichte b ermöglicht. Die Modellparameter werden dabei so gewählt, dass die Summe der quadrierten Fehler (= Abweichungen der beobachteten Y-Werte von den durch das Modell vorhergesagten Kriteriumswerten Xb) ein Minimum erreicht: | Die gleichzeitige Betrachtung der Werte mehrerer Beobachtungseinheiten (z.B. Individuen) führt zu einem linearen Gleichungssystem, welches mit Hilfe eines Minimierungsprinzips (dem Prinzip der Kleinsten Quadrate) die Schätzung der gesuchten Prädiktorgewichte b ermöglicht. Die Modellparameter werden dabei so gewählt, dass die Summe der quadrierten Fehler (= Abweichungen der beobachteten Y-Werte von den durch das Modell vorhergesagten Kriteriumswerten Xb) ein Minimum erreicht: | ||
| Zeile 28: | Zeile 28: | ||
{| | {| | ||
| | | [[Datei:GLM_4.png]] | ||
| Schätzung von b | | Schätzung von b | ||
|- | |- | ||
| | | [[Datei:GLM_5.png]] | ||
| inverse Matrix von | | inverse Matrix von [[Datei:GLM_7.png]] | ||
|- | |- | ||
| | | [[Datei:GLM_6.png]] | ||
| Transposition der Matrix X | | Transposition der Matrix X | ||
|} | |} | ||
Version vom 25. August 2018, 20:39 Uhr
Das General Linear Model (dt. Allgemeines Lineares Modell, ALM) ist ein grundlegendes Modell der Statistik, auf welchem eine Vielzahl häufig eingesetzter Verfahren, wie z.B. die Varianzanalyse, die Regressionsanalyse und viele weitere Verfahren basieren. Sie alle stellen Spezialfälle des GLM dar.
Es ermöglicht die Beschreibung der Ausprägungen einer oder mehrerer Kriteriumsvariablen (= abhängiger Variablen) durch eine Linearkombination (gewichtete Summe) von Prädiktorvariablen (= unabhängiger Variablen) und einer Fehlerkomponente (Residuum). Die unabhängigen Variablen bilden den Ausgangspunkt für die Vorhersage und werden daher Prädiktoren genannt. Die abhängige Variable, dessen Ausprägung man vorhersagen möchte, wird in der Psychologie als Kriteriumsvariable bezeichnet. Grundvoraussetzung für die Anwendung des Modells ist die Annahme, dass ein linearer Zusammenhang zwischen den zu erklärenden Beobachtungsdaten und den bekannten Einflussvariablen (Prädiktoren / Regressoren) besteht.
Formal lässt sich das GLM durch die folgende Gleichung beschreiben:
Y... Vektor der Kriteriumsvariablen
X... Matrix der Prädiktoren (= Designmatrix)
b... Vektor der Gewichte aller Prädiktoren
e... Vektor der Residuen
Die gleichzeitige Betrachtung der Werte mehrerer Beobachtungseinheiten (z.B. Individuen) führt zu einem linearen Gleichungssystem, welches mit Hilfe eines Minimierungsprinzips (dem Prinzip der Kleinsten Quadrate) die Schätzung der gesuchten Prädiktorgewichte b ermöglicht. Die Modellparameter werden dabei so gewählt, dass die Summe der quadrierten Fehler (= Abweichungen der beobachteten Y-Werte von den durch das Modell vorhergesagten Kriteriumswerten Xb) ein Minimum erreicht:
- n... Anzahl an Individuen
Als beste Schätzung für b erhält man durch Formelumstellung:
| Datei:GLM 4.png | Schätzung von b |
| Datei:GLM 5.png | inverse Matrix von Datei:GLM 7.png |
| Datei:GLM 6.png | Transposition der Matrix X |