Modelltypen

Modelle stellen Abbilder von realen Systemen dar. Sie versuchen die Komplexität der Realität vereinfacht darzustellen und fokussieren dabei auf wesentliche Merkmale und Relationen. Welche Aspekte als relevant betrachtet werden ist abhängig vom Ziel der Modellierung. Doch was kann man sich nun konkret unter Modellen vorstellen? Worin unterscheiden sie sich?

Eine erste grobe Einteilung könnte folgendermaßen aussehen:

• Realmodelle: z.B. eine Maus mit einer Mutation auf dem NLGN3-Gen als „Tiermodell“ für Autismus
• Ikonische (anschauliche) Modelle: z.B. Modelleisenbahn oder eine architektonische Zeichnung
• Verbalmodelle: eine verbale Theorie in natürlicher Sprache: z.B. Dissonanztheorie
• Formalmodelle: mathematische Gleichungen oder Computerprogramme, z.B. Rescorla-Wagner Modell

In der Psychologie sind Verbalmodelle aktuell noch am weitesten verbreitet, allerdings nimmt der Anteil formalisierter Modelle stetig zu, was aufgrund ihrer vielen Vorteile und im Vergleich zu anderen Naturwissenschaften als Fortschritt angesehen wird (vgl. z.B. Stellungnahme des Wissenschaftsrates) . Der Fokus dieses Moduls wird deshalb auf Formalmodellen und deren unterschiedlichen Ausprägungen liegen.

Es gibt eine große Vielzahl verschiedener Modelle und diese lassen sich anhand verschiedener Aspekte unterscheiden. Die Kenntnis dieser Unterscheidungen hilft ein Modell zu finden, das optimal zum eigenen Erkenntnisinteresse passt.

Abgrenzung nach Zweck und Komplexität

Formalmodelle lassen sich nach Michael Dawson unterteilen in:

• Statistische Modelle
• Mathematische Modelle
• Synthetische / Explanative Modelle

Diese Modelltypen besitzen unterschiedliche Merkmale, welche in den folgenden Artikeln näher beschrieben werden. Aufgrund ihrer spezifischen Eigenschaften eignen sie sich für verschiedene Anwendungssituationen. Statistische Modelle etwa sind in der empirisch ausgerichteten Psychologie zur Beschreibung von Daten bestimmter Fälle weit verbreitet, zur Theoriebildung im Sinne einer Abstraktion konkreter Daten jedoch nur bedingt geeignet. Dies ist hingegen mittels mathematischer und komputationaler Modelle möglich.

Abgrenzung durch Analyseebene

Viele Einteilungssysteme unterscheiden Modelle anhand einer wichtigen Entscheidung, die man beim Modellieren treffen muss: auf welcher Ebene (Abstraktion) will man ein System betrachten und analysieren? Modelle unterscheiden sich also auch darin, auf welche Abstraktions- oder Analyseebene sie abzielen.

Der britische Psychologe, Mathematiker und Informatiker David Marr schlug vor, Informationsverarbeitungssysteme, wie zum Beispiel das visuelle System, auf drei unterschiedlichen, komplementären Ebenen zu analysieren:

• Komputationale Ebene (computational level): Was tut das System? Welchen Zweck, welche Logik, welche Strategien verfolgt es dabei?
• Algorithmische Ebene (algorithmic level): Wie arbeitet das System? Mit welchen Repräsentationen arbeitet es und welche Prozesse wendet es zur Erzeugung und Transformation dieser Repräsentationen an?
• Technische oder Implementierungsebene (implementational level): Wie ist das System physikalisch realisiert? (für Kognitionen: Durch welche neuronalen Strukturen oder Prozesse wird das Phänomen implementiert?)

Da die Ebenen nur leicht miteinander verknüpft sind, sind sie relativ unabhängig voneinander. Trotzdem empfahl Marr einen Top-Down Ansatz bei der Modellbildung, d.h. bei der abstrakteren komputationalen Ebene anzufangen und sukzessive ins Detail zu gehen.

Einen ähnlichen Drei-Ebenen-Ansatz für kognitive Modelle verfolgten Newell und Simon (1976):

• Wissensebene: erklärt das Systemverhalten durch Berufung auf dessen Ziele und Wissen
• Symbolebene: hier werden Ziele und Wissen in Symbole enkodiert und durch deren Manipulation miteinander verbunden
• Physische Ebene: physikalische Realisierung der Symbolstrukturen und deren Manipulation

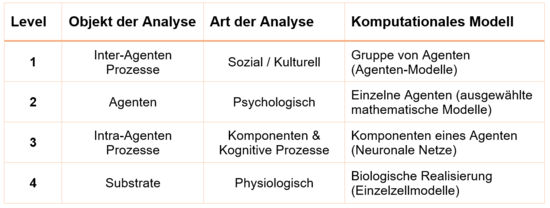
Ron Sun und Kollegen (2006) postulierten dagegen einen sehr anderen Ansatz, der stärker auf die Unterscheidung der zu untersuchenden Phänomene, also deren Wirkungsbereich, Größenordnung oder Grad der Abstraktion fokussiert. Die daraus resultierenden Unterschiede in der Analyse decken sich mit den unterschiedlichen wissenschaftlichen Disziplinen, von der mikroskopischen zur makroskopischen Ebene. Folgende Ebenen der Analyse werden dabei unterschieden:

• Soziologische Ebene: kollektives Verhalten von Agenten, Inter-Agenten-Prozesse, soziokulturelle Prozesse, Agenten-Umwelt-Interaktionen
• Psychologische Ebene: individuelles Verhalten, Annahmen, Wissen, Konzepte, Fähigkeiten (inklusive Wahrnehmung, Emotion etc.)
• Komponenten Ebene: symbolische Berechnungen, konnektionistische/neuronale Netze, semantische Netzwerke
• Physiologische Ebene: biologische Substrate, neuronale Aktivierungen, strukturelle Unterschiede

Laut Sun können sich alle Ebenen wechselseitig wichtigen Input liefern, sich also sowohl bottom-up (biologische Grenzen einer kognitiven Theorie) als auch top-down (Einbettung individuellen Verhaltens in soziale Normen und Werte) informieren und beschränken.

Auf die potentielle Kritik, ein bestimmtes Modell oder (kognitive) Modelle allgemein wären in ihrer Erklärungskraft zu eingeschränkt und würden ein Phänomen nicht in seiner Gänze fassen, lässt sich ggf. entgegnen, dass ein Modell i.d.R. nur eine oder wenige Ebenen der Betrachtung einnimmt und generell auch nicht alle diese erfüllen kann, weshalb für ein umfassendes Verständnis des Phänomens natürlich auch die anderen Ebenen berücksichtigt werden müssen.

Abgrenzung durch das Ziel der Modellierung: Auswertung vs. Theoriebildung

Modelle können zudem darin unterschieden werden, an welcher Stelle des Forschungsprozesses sie eingesetzt werden. So dienen manche Modelle vorrangig als reine Auswertungsmethode: Sie dienen zur sparsamen Beschreibung der Daten oder zur Analyse oberflächlich versteckter Zusammenhänge. Andere Modelle hingegegen dienen vorrangig als Instrument zur Theorie- und Hypothesenbildung: Sie unterstützen Wissenschaftler dabei, ihre Theorien zu entwickeln, zu spezifizieren und Vorhersagen abzuleiten.

Diese ganz andere Kategorisierung von Modellen ist nicht ganz unabhängig von den anderen Kategorisierungsarten und kann verwirrend erscheinen, wenn wir z.B. die Einteilung von Dawson in statistische und mathematische Modelle betrachten. Statistische Modelle werden i.d.R. als reine Auswertungsmethode verwendet, um bestimmte Daten zusammenzufassen und interpretierbare Parameter daraus zu extrahieren, z.B. den Mittelwert und die Streuung. Mathematische Modelle hingegen werden i.d.R. als theoriebildende Modelle verwendet. Für beide ist aber eine gegenteilige Verwendung nicht ausgeschlossen. Zum Beispiel wird das Diffusions Modell oft dafür genutzt, Parameter wie die Drift Rate aus empirischen Daten zu gewinnen. Der Vorteil liegt auf der Hand, denn das Modell berücksichtigt sowohl Reaktionszeitdaten als auch die Reaktionskorrektheit und beschreibt folglich die Daten besser als ein reiner Reaktionszeit-Mittelwert. In dieser Hinsicht könnte man es nach Dawson als statistisches Modell einordnen; es wäre eine etwas komplexere Auswertungsmethode, die einem hilft, latente Variablen zu identifizieren (ähnlich z.B. einer Faktoranalyse). Allerdings ist es auch (eingeschränkt) möglich, dieses Modell zur Theorienbildung zu verwenden, etwa indem die Parameter oder ihre Relation modifiziert oder uminterpretiert werden, oder indem zusätzliche Drifteinflüsse angenommen werden, die verschieden schnelle kognitive Prozesse widerspiegeln. Solchen Modifikationen spiegeln theoretische Annahmen wider und aus ihnen lassen sich neue Vorhersagen ableiten, die dann empirisch geprüft werden können. In dieser Hinsicht könnte man das Modell nach Dawson auch als mathematisches Modell einordnen, denn es beschreibt einen kognitiven Prozess mit mathematischen Mitteln und unterstützt so die Theoriebildung.