Mehrfaktorielle Versuchspläne: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Elisa (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
||
| (3 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 11: | Zeile 11: | ||
In mehrfaktoriellen Designs werden sämtliche Faktorstufen miteinander kombiniert, beispielsweise in einer Kreuztabelle: | In mehrfaktoriellen Designs werden sämtliche Faktorstufen miteinander kombiniert, beispielsweise in einer Kreuztabelle: | ||
{| class="wikitable" style="text-align:center;" | |||
|- style="font-weight:bold;" | |||
! | |||
! A<sub>1</sub> | |||
! A<sub>2</sub> | |||
|- | |||
! B<sub>1</sub> | |||
| A<sub>1</sub> B<sub>1</sub> | |||
| A<sub>2</sub> B<sub>1</sub> | |||
|- | |||
! B<sub>2</sub> | |||
| A<sub>1</sub> B<sub>2</sub> | |||
| A<sub>2</sub> B<sub>2</sub> | |||
|} | |||
In jeder Zelle befindet sich jetzt eine Faktorstufenkombination. Für diese braucht man jeweils eine Untersuchungsstichprobe. In einem 2x2-faktoriellen Design benötigt man 4 Gruppen, in einem 2x3x2-faktoriellen Design benötigt man schon 12 Gruppen. Nach Sarris (1992) sollte man in einem mehrfaktoriellen Randomisierungsdesign pro Zelle etwa 5-15 Versuchspersonen einplanen. Die Präzision steigt dabei mit zunehmender Probandenanzahl. | In jeder Zelle befindet sich jetzt eine Faktorstufenkombination. Für diese braucht man jeweils eine Untersuchungsstichprobe. In einem 2x2-faktoriellen Design benötigt man 4 Gruppen, in einem 2x3x2-faktoriellen Design benötigt man schon 12 Gruppen. Nach Sarris (1992) sollte man in einem mehrfaktoriellen Randomisierungsdesign pro Zelle etwa 5-15 Versuchspersonen einplanen. Die Präzision steigt dabei mit zunehmender Probandenanzahl. | ||
| Zeile 33: | Zeile 46: | ||
Als Design wird ein 2x2-faktorielles Design mit Randomisierung verwendet. Aus der Kreuztabelle werden die 4 Faktorstufenkombinationen ersichtlich: | Als Design wird ein 2x2-faktorielles Design mit Randomisierung verwendet. Aus der Kreuztabelle werden die 4 Faktorstufenkombinationen ersichtlich: | ||
[[Datei: Mehrfaktoriell Beispiel Glas.jpg|391px]] | [[Datei: Mehrfaktoriell Beispiel Glas.jpg|391px|link=Ausgelagerte_Bildbeschreibungen#Mehrfaktoriell_Beispiel_Glas|Ausgelagerte Bildbeschreibung von Mehrfaktoriell Beispiel Glas]] | ||
Pro Faktorstufenkombination sollen mindestens 10 Versuchspersonen untersucht werden. Es werden also insgesamt 2 x 2 x 10 = 40 Versuchspersonen benötigt. Das zugrunde liegende Design sieht folgendermaßen aus: | Pro Faktorstufenkombination sollen mindestens 10 Versuchspersonen untersucht werden. Es werden also insgesamt 2 x 2 x 10 = 40 Versuchspersonen benötigt. Das zugrunde liegende Design sieht folgendermaßen aus: | ||
[[Datei: Mehrfaktoriell Glas Plan.jpg|450px]] | [[Datei: Mehrfaktoriell Glas Plan.jpg|450px|link=Ausgelagerte_Bildbeschreibungen#Versuchsplan_Glas|Ausgelagerte Bildbeschreibung von Versuchsplan Glas]] | ||
Aktuelle Version vom 9. Dezember 2021, 15:07 Uhr
"Unter einem mehrfaktoriellen Versuchsplan versteht man die Verallgemeinerung der unifaktoriellen Versuchsplanung auf den Fall des Einflusses von zwei, drei oder mehr unabhängigen Faktoren in ein und derselben Versuchsanordnung“ (Sarris, 1992, S.75)
In mehrfaktoriellen Plänen werden also zwei oder mehr unabhängige Variablen (Faktoren) untersucht. Diese werden mit A, B, C, usw. bezeichnet und sind zwei oder mehrfach gestuft. Für jeden dieser Faktoren müssen Kontrollstrategien festgelegt werden. Verwendet man für verschiedene Faktoren unterschiedliche Kontrollstrategien, spricht man von Mischversuchsplänen. Wird die gleiche Kontrollstrategie für alle Faktoren verwendet, so liegt eines der folgenden Designs vor:
- alle Faktoren sind randomisiert (R): independent factorial design
- oder bei allen Faktoren wird Blockbildung vorgenommen (Bl): matched factorial design
- oder alle Faktoren werden über Messwiederholung kontrolliert (W): repeated measures factorial design
Der einfachste Fall eines mehrfaktoriellen Plans ist ein 2x2-faktorielles Design. In diesem werden 2 Faktoren erforscht, die jeweils zweifach gestuft sind. Die Zahlen in der Bezeichnung geben jeweils die Anzahl der Stufen an, die Menge der Zahlen gibt Auskunft über die Menge der Faktoren. Ein 3x4x5 Design ist entsprechend ein dreifaktorielles Design mit einem Faktor à 3 Stufen, einem á 4 Stufen und einem à 5 Stufen.
In mehrfaktoriellen Designs werden sämtliche Faktorstufen miteinander kombiniert, beispielsweise in einer Kreuztabelle:
| A1 | A2 | |
|---|---|---|
| B1 | A1 B1 | A2 B1 |
| B2 | A1 B2 | A2 B2 |
In jeder Zelle befindet sich jetzt eine Faktorstufenkombination. Für diese braucht man jeweils eine Untersuchungsstichprobe. In einem 2x2-faktoriellen Design benötigt man 4 Gruppen, in einem 2x3x2-faktoriellen Design benötigt man schon 12 Gruppen. Nach Sarris (1992) sollte man in einem mehrfaktoriellen Randomisierungsdesign pro Zelle etwa 5-15 Versuchspersonen einplanen. Die Präzision steigt dabei mit zunehmender Probandenanzahl. Durch die Untersuchung von mehr als einer unabhängige Variable gewinnt das Experiment an Komplexität. So können nicht nur Aussagen über die Wirkung der einzelnen Variablen (Haupteffekte), sondern auch über deren kombinierte Wirkung (Interaktionseffekte) gemacht werden. Entsprechend müssen auch mehrere Hypothesen formuliert werden: eine Hypothese für jeden Faktor und eine Hypothese für jede Kombination von mind. 2 Faktoren. Im 2x2-Design können insgesamt 3 Hypothesen untersucht werden: a) Hypothese über den Haupteffekt von Faktor A. b) Hypothese über den Haupteffekt von Faktor B. c) Hypothese über den Interaktionseffekt von Faktor A x Faktor B. In den zweifaktoriellen Designs können also mehr experimentell-statistische Daten und Informationen gewonnen werden. Je mehr Faktoren hinzukommen, umso aufwändiger wird ein mehrfaktorielles Design. Beispielsweise werden in einem dreifaktoriellen Design bereits 7 Hypothesen untersucht: a) Hypothese über den Haupteffekt von Faktor A. b) Hypothese über den Haupteffekt von Faktor B. c) Hypothese über den Haupteffekt von Faktor C. d) Hypothese über den Interaktionseffekt von Faktor A x Faktor B. e) Hypothese über den Interaktionseffekt von Faktor A x Faktor C. f) Hypothese über den Interaktionseffekt von Faktor C x Faktor B. g) Hypothese über den Interaktionseffekt von Faktor A x Faktor B x Faktor C. Die Interpretation solcher Interaktionen wird mit steigender Faktorzahl zunehmend kollektiver. Abgesehen davon nimmt die Anzahl der benötigten Versuchspersonen exponentiell zu, wodurch die Kosten steigen. Es ist daher notwendig bei der Verwendung von mehrfaktoriellen Designs Kosten und Nutzen sorgfältig abzuwägen. Es ist außerdem zu überlegen, durch eine andere geeignete Kontrollstrategie (Wiederholungsmessung oder Blockbildung) Versuchspersonen einzusparen.
Beispiel:
In einem Experiment wird der Einfluss von Kaffee (1. Faktor) und Milch (2. Faktor) auf die Konzentrationsleistung untersucht. Hierfür soll ein Teil der Versuchspersonen Kaffee trinken, der andere nicht. Zusätzlich soll ein Teil der Versuchspersonen Milch trinken und der andere nicht. Im Anschluss wird ein kurzer Konzentrationsleistungstest gemacht.
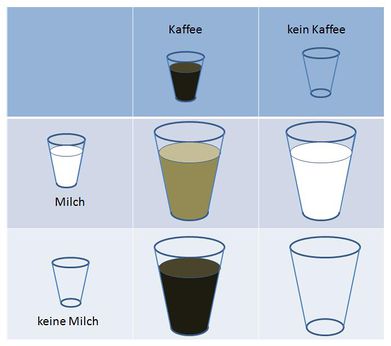
Als Design wird ein 2x2-faktorielles Design mit Randomisierung verwendet. Aus der Kreuztabelle werden die 4 Faktorstufenkombinationen ersichtlich:
Pro Faktorstufenkombination sollen mindestens 10 Versuchspersonen untersucht werden. Es werden also insgesamt 2 x 2 x 10 = 40 Versuchspersonen benötigt. Das zugrunde liegende Design sieht folgendermaßen aus: