Korrelation: Unterschied zwischen den Versionen
Diana (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 12: | Zeile 12: | ||
'''Wichtig: Die Korrelation ist nur eine deskriptive Beziehung zwischen den Variablen, es kann hier keine Aussage über einen Kausalzusammenhang getroffen werden! ''' | '''Wichtig: Die Korrelation ist nur eine deskriptive Beziehung zwischen den Variablen, es kann hier keine Aussage über einen Kausalzusammenhang getroffen werden! ''' | ||
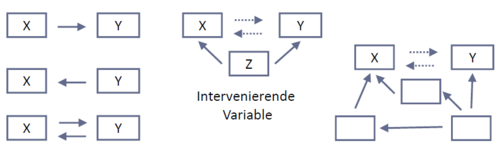
<br/>Aus einer Korrelation zwischen zwei Variablen kann nicht etwa geschlossen werden, dass sich Variable X in bestimmter Weise auf Variable Y auswirkt. Eine gemeinsame Veränderung kann unzählige andere Ursachen haben: | <br/>Aus einer Korrelation zwischen zwei Variablen kann nicht etwa geschlossen werden, dass sich Variable X in bestimmter Weise auf Variable Y auswirkt. Eine gemeinsame Veränderung kann unzählige andere Ursachen haben: | ||
[[Datei:Korrelation3.png|500px]] | [[Datei:Korrelation3.png|500px]] | ||
Version vom 22. Februar 2015, 20:02 Uhr
Eine Korrelation bezeichnet den Zusammenhang zwischen zwei oder mehr Variablen. Dieser Zusammenhang kann positiv oder negativ sein.

Die Korrelation wird häufig durch den Buchstaben r ausgedrückt. Der Wert von r liegt immer zwischen -1 und 1.
Bei einem positiven Zusammenhang (d.h. mit höherem Wert der Variable A steigt auch der Wert der Variable B) ist der Wert größer als null, bei einem negativen Zusammenhang (d.h. mit höherem Wert der Variable A sinkt der Wert der Variable B) kleiner als Null und bei keinerlei Zusammenhang der Variablen beträgt r exakt 0.
Die Stärke des Zusammenhangs wird hierbei durch den Abstand von 0 gekennzeichnet. Normalerweise gelten Korrelationen mit einem Betrag von unter 0,3 als schwach und Korrelationen mit einem Betrag ab 0,5 als stark.
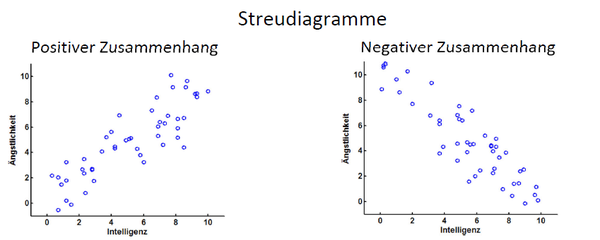
In Streudiagrammen gilt grundsätzlich: je mehr die Punktwolke einer Geraden gleicht, desto stärker ist der Zusammenhang – je mehr sie einem Kreis gleicht, desto schwächer ist er. Starke Korrelationen sehen beispielsweise folgendermaßen aus:
Wichtig: Die Korrelation ist nur eine deskriptive Beziehung zwischen den Variablen, es kann hier keine Aussage über einen Kausalzusammenhang getroffen werden!
Aus einer Korrelation zwischen zwei Variablen kann nicht etwa geschlossen werden, dass sich Variable X in bestimmter Weise auf Variable Y auswirkt. Eine gemeinsame Veränderung kann unzählige andere Ursachen haben: